Question
Random sample. 2. Suppose 42% of Ph.D.s in statistics/biostatistics are earned by woman and a random sample 36 statistics/iostatistics Ph.D.s is obtained.(You may want to

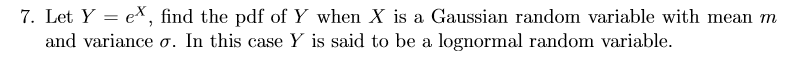

Random sample.
2. Suppose 42% of Ph.D.s in statistics/biostatistics are earned by woman and a random sample 36 statistics/iostatistics Ph.D.s is obtained.(You may want to use technology to compute some of the probabilities.)
a. What's the probability none of the 36 statistics/biostatistics Ph.D.s are women?
b. What's the probability at least 1 of the 36 statistics/biostatistics Lh.D.s is a woman?
c. How many woman do you expect in the sample of the 36 statistics/biostatistics Ph.D.s?
d. What's the probability fewer than half of hte 36 statistics/biostatistics Ph.D.s are women?
e. What's the probability fewer than half of the 36 statistics/biostatistics Ph.D.s are women if at least 12 are not women?
f. What's the probability the first woman is the 5th person in the sample?
g. What's the probability the first woman is the 15th person in the sample?


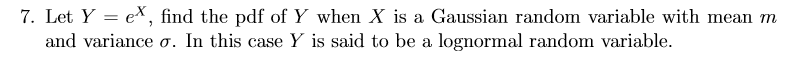

Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


