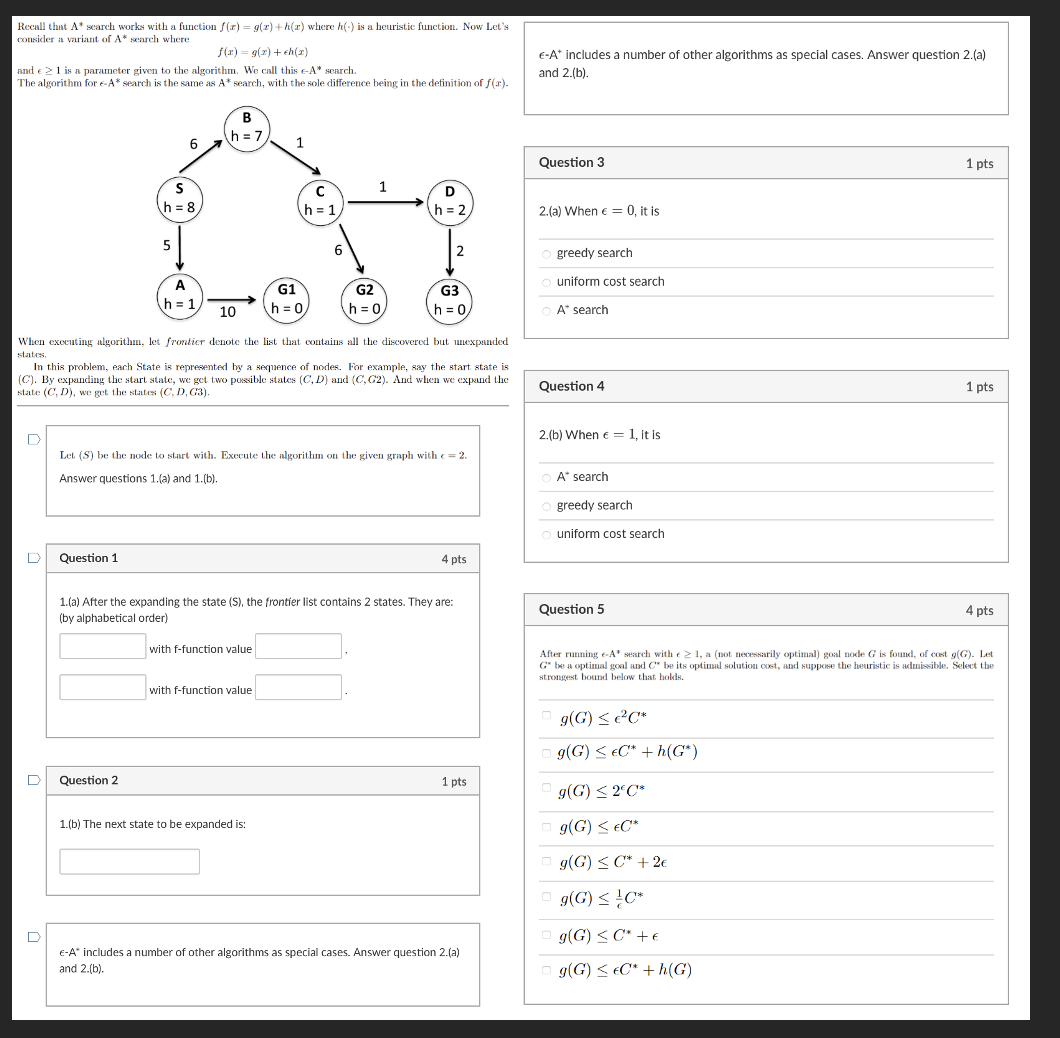
Recall that ${}^{**}$ scarch works with a function $f(x)=g(x)+h(x)$ where $h(*)$ is a heuristic function. Now Let's

consider a variant of $A^{**}$ search where

$f(x)=g(x)+lonh(x)$

and $lon1$ is a parameter given to the algorithm. We call this $lon-A^{**}$ search.

The algorithm for $lon-A^{**}$ search is the same as $A^{**}$ search, with the sole difference being in the definition of $f(x).$

When executing algorithm, let frontier denote the list that contains all the discovered but unexpunded

states,

In this problem, each State is represented by a sexpuence of nodes. For example, say the start state is

$(C).$ By expending the start state, we get two porsible states $(C,D)$ and $(C,C2).$ And when we expand the

state $(C,D),$ we get the states $(C,D,G3).$

Let $(S)$ be the node to start with. Exceute the algorithm on the given graph with $c=2.$

Answer questions $1.($a$)$ and $1.($b$).$

Question $1$

$4$ pts

$1.($a$)$ After the expanding the state $($S$),$ the frontier list contains $2$ states. They are:

$($by alphabetical order$)$

with f$-$function value

with f$-$function value

Question $2$

$1pts$

$1.($b$)$ The next state to be expanded is:

$lon-A^{**}$ includes a number of other algorithms as special cases. Answer question $2.($a$)$

and $2.($b$).$

$lon-A^{+}$includes a number of other algorithms as special cases. Answer question $2.($a$)$

and $2.($b$).$

Question $3$

$2.($a$)$ When $lon=0,$ it is

greedy search

uniform cost search

$A^{+}$search

Question $4$

$2.($b$)$ When $lon=1,$ it is

$A^{**}$ search

greedy search

uniform cost search

Question $5$

After running $lon-A^{+}$search with $lon1,$ a $($not necessarily optimal$)$ goal node $G$ is found, of cost $g(G).$ Let

$G^{**}$ be a optimal goal and $C^{**}$ be its optimal solution cost, and suppose the heuristic is admissible. Select the

strongest bound below that holds.