Refer to Example 8.5. In many situations in which the difference in variances is not too great, the results from the AOV comparisons of the population means of the transformed data are very similar to the results that would have been obtained using the original data. In these situations, the researcher is inclined to ignore the transformations because the scale of the trans- formed data is not relevant to the researcher. Thus, confidence intervals constructed for the means using the transformed data may not be very relevant. One possible remedy for this problem is to construct confidence intervals using the transformed data and then perform an inverse transformation of the endpoints of the intervals. Then we would obtain a confidence interval with values having the same units of measurement as the original data.

a. Test the hypothesis that the mean hours of relief for patients from the three treatments differs using a ?=.05. Use the original data.

b. Place 95% confidence intervals on the mean hours of relief for the three treatments.

c. Repeat the analysis in parts (a) and (b) using the transformed data.

d. Comment on any differences in the results of the test of hypotheses.

e. Perform an inverse transformation on the endpoints of the intervals constructed in part (c). Compare these intervals to the ones constructed in part (b).

EXAMPLE 8.5

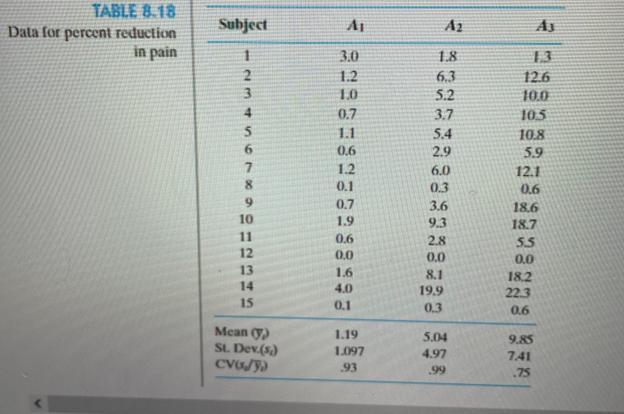
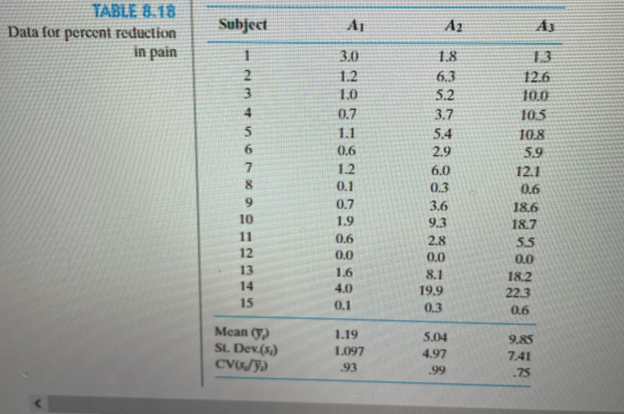
Arthritis is a very commonly occurring affliction. It is a major cause of lost work time and often results in serious disability. Of the many types of arthritis, the most common type is osteoarthritis. This condition is frequently due to wear and tear in the joints and is more likely to be found in people over 50. It is very painful in the weight-bearing joints, such as the knees and hips. Cartilage wears away on the bone ends, causing pain and swelling. Osteoarthritis may develop after an injury such as a bone fracture or a joint dislocation. In order to reduce the amount of time osteoarthritis patients are absent from work, it is important for them to have effective pain relief. An experiment was conducted to compare the effectiveness of three new analgesics: A1, A2, and A3. A clinic evaluated a large group of patients and identified 45 patients with a moderate level of pain. Fifteen of the 45 persons were then randomly assigned to one of the three analgesics. The patients were then placed on the therapies, and the percentage reduction in pain level was assessed for each patient. These values are recorded in Table 8.18.

a. Are there significant differences among the population variances for the three analgesics? Use a 5 .05.

b. Does it appear that the coefficient of variation is constant across the three therapies? If yes, then apply the log transformation to the data to try to stabilize the variances.

c. Compute the sample means and sample standard deviations for the transformed data. Did the transformation yield a stabilization of the variances?

TABLE 8.18 Subject A2 Data for percent reduction in pain 1.8 6.3 126 5.2 10.0 3.7 105 5.4 10.8 2.9 5.9 6.0 12.1 03 0.6 3.6 18.6 9.3 18.7 2.8 5.5 0.0 0.0 8.1 18.2 19.9 22.3 0.3 0.6 Mean ( 1.19 5.04 9.85 SL Dev.(5) 1.097 4.97 7.41 93 .99 .75