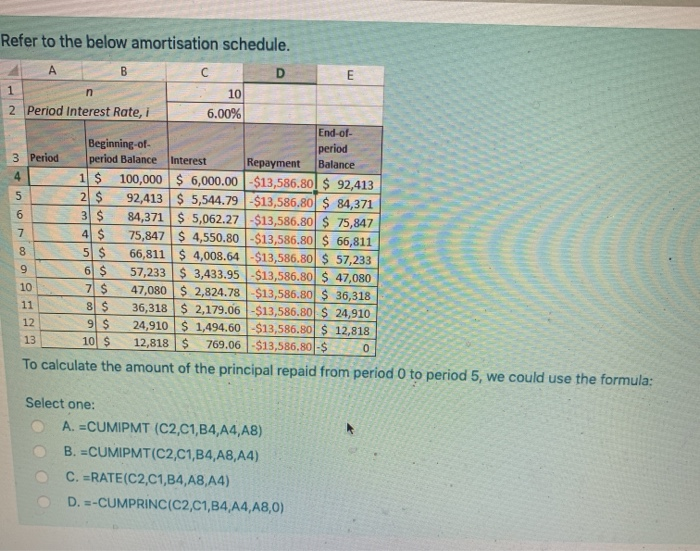
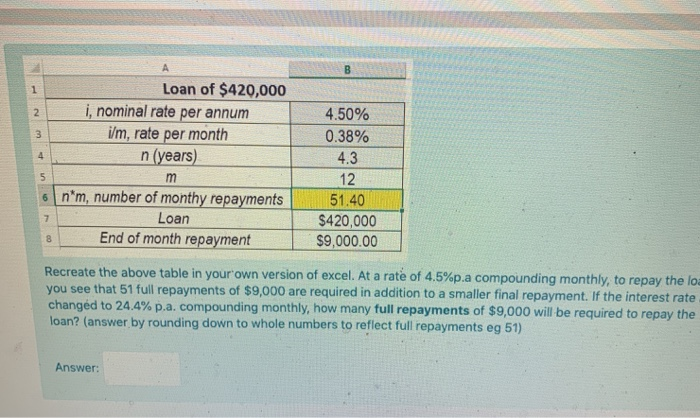
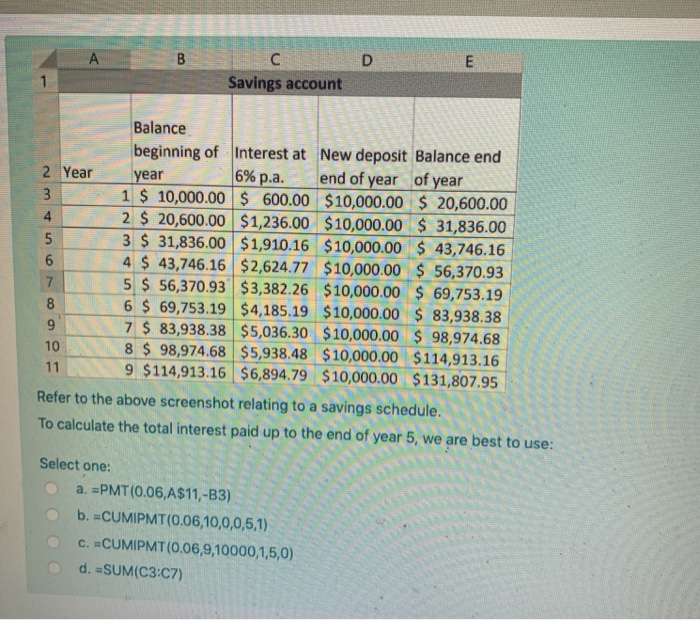
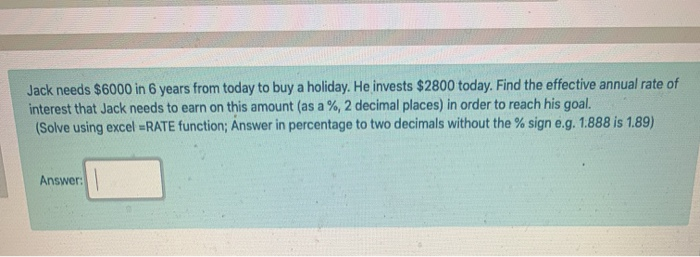
Refer to the below amortisation schedule. A B D E 2 1 n 10 2 Period interest Rate, i 6.00% End-of- Beginning-of- period 3 Period period Balance Interest Repayment Balance 4 1 $ 100,000 $ 6,000.00 $13,586.80 $ 92,413 5 2 $ 92,413 $ 5,544.79 -$13,586.80 $ 84,371 6 3 $ 84,371 $ 5,062.27 - $13,586.80 $ 75,847 7 4 $ 75,847 $ 4,550.80 -$13,586.80 $ 66,811 8 5 $ 66,811 $ 4,008.64 $13,586.80 $ 57,233 9 6 $ 57,233 $ 3,433.95 $13,586.80 $ 47,080 10 7 $ 47,080 $ 2,824.78 $13,586.80 $ 36,318 11 8 $ 36,318 $ 2,179.06 -$13,586.80 $ 24,910 12 9 $ 24,910 $ 1,494.60 $13,586.80 $ 12,818 13 10 $ 12,818 $ 769.06 $13,586,80 $ 0 To calculate the amount of the principal repaid from period 0 to period 5, we could use the formula: Select one: A. =CUMIPMT (C2,C1,B4,A4,A8) B. =CUMIPMT(C2,C1,B4, A8, A4) C. =RATE(C2,C1,B4, A8, A4) D. E-CUMPRINC(C2,C1,B4, A4, A8,0) A B 1 3 4 5 Loan of $420,000 2 i, nominal rate per annum 4.50% ilm, rate per month 0.38% n (years) 4.3 m 12 6 nm, number of monthy repayments 51.40 Loan $420,000 8 End of month repayment $9,000.00 Recreate the above table in your own version of excel. At a rate of 4.5%p.a compounding monthly, to repay the loa you see that 51 full repayments of $9,000 are required in addition to a smaller final repayment. If the interest rate changed to 24.4% p.a. compounding monthly, how many full repayments of $9,000 will be required to repay the loan? (answer by rounding down to whole numbers to reflect full repayments eg 51) 7 Answer: A B D E E C Savings account 6% p.a. 5 Balance beginning of Interest at New deposit Balance end 2 Year year end of year of year 3 1 $ 10,000.00 $ 600.00 $10,000.00 $ 20,600.00 4 2 $ 20,600.00 $1,236.00 $10,000.00 $ 31,836.00 3 $ 31,836.00 $1,910.16 $10,000.00 $ 43,746.16 6 4 $ 43,746.16 $2,624.77 $10,000.00 $ 56,370.93 7 5 $ 56,370.93 $3,382.26 $10,000.00 $ 69,753.19 8 6 $ 69,753.19 $4,185.19 $10,000.00 $ 83,938.38 9 7 $ 83,938.38 $5,036.30 $10,000.00 $ 98,974.68 10 8 $ 98,974.68 $5,938.48 $10,000.00 $114,913.16 11 9 $114,913.16 $6,894.79 $10,000.00 $131,807.95 Refer to the above screenshot relating to a savings schedule. To calculate the total interest paid up to the end of year 5, we are best to use: Select one: a. =PMT(0.06, A$11,-B3) b. CUMIPMT(0.06,10,0,0,5,1) C. CUMIPMT(0.06,9,10000,1,5,0) d. =SUM(C3:07) Jack needs $6000 in 6 years from today to buy a holiday. He invests $2800 today. Find the effective annual rate of interest that Jack needs to earn on this amount (as a %, 2 decimal places) in order to reach his goal. (Solve using excel =RATE function; Answer in percentage to two decimals without the % signe.g. 1.888 is 1.89)