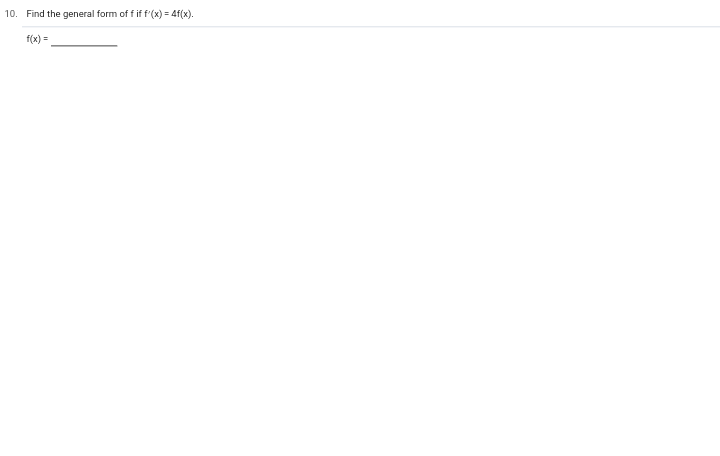
Reference: : Calculus and Its Applications, 12th, by Marvin L. Bittinger and David Ellenbogen Book
These are practice questions with unlimited attempts but I need help learning the problems
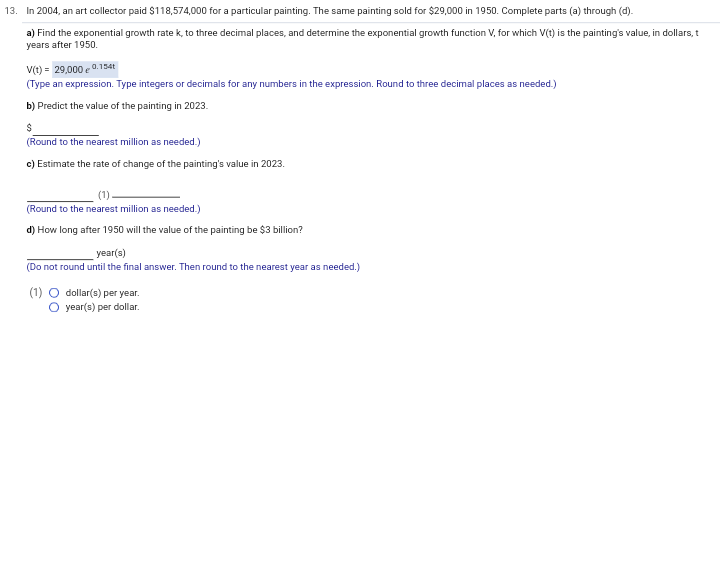
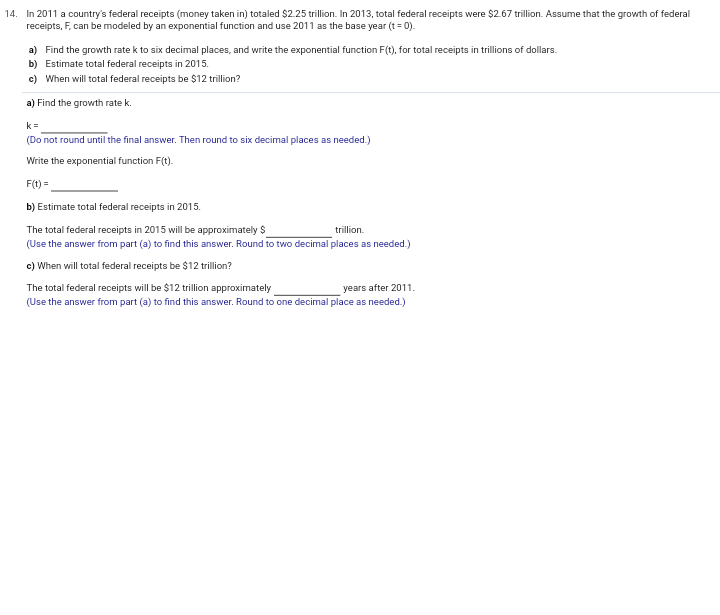
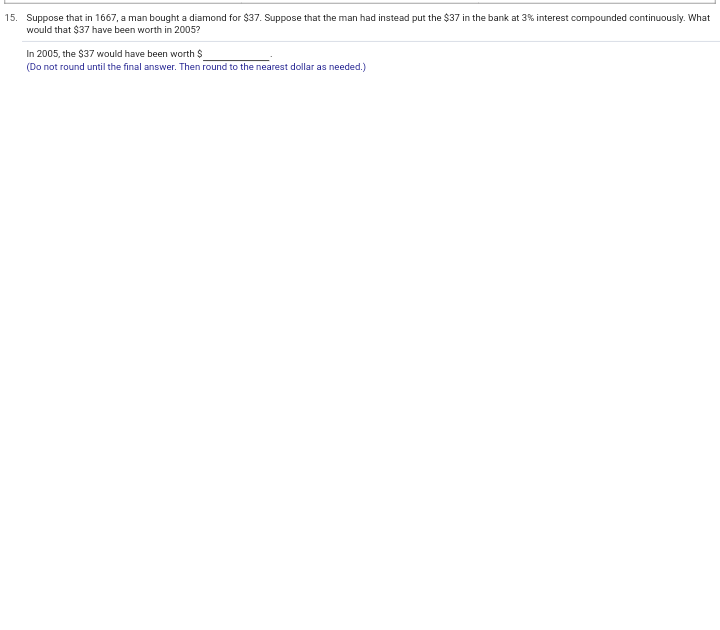
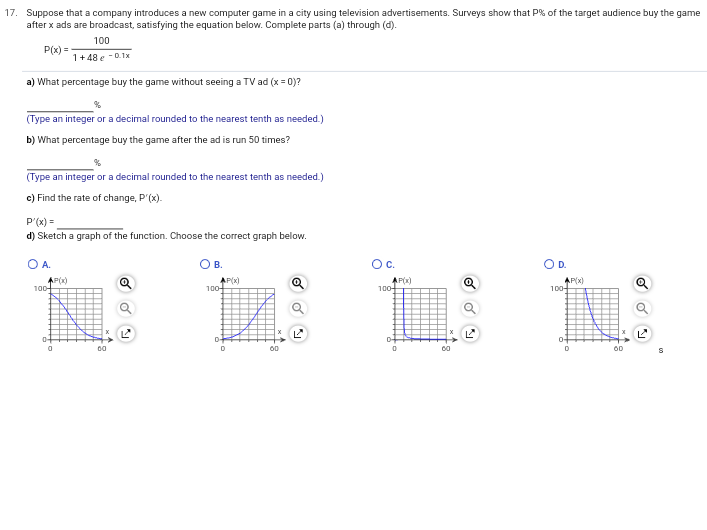
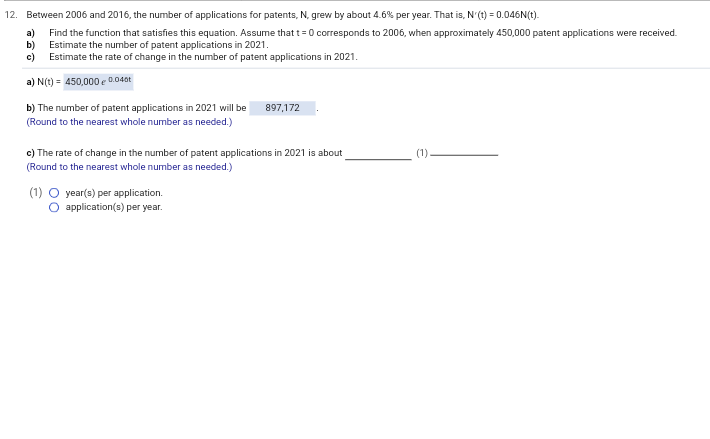
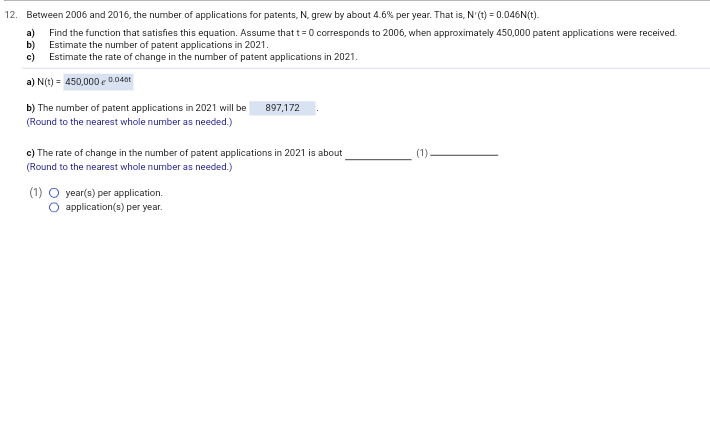
\f13. In 2004, an art collector paid $118,574,000 for a particular painting. The same painting sold for $29,000 in 1950. Complete parts (a) through (d). a) Find the exponential growth rate k, to three decimal places, and determine the exponential growth function V, for which V(t) is the painting's value, in dollars, t years after 1950. V(t) = 29,000 e 0.154t (Type an expression. Type integers or decimals for any numbers in the expression. Round to three decimal places as needed.) b) Predict the value of the painting in 2023. (Round to the nearest million as needed.) c) Estimate the rate of change of the painting's value in 2023. (1). (Round to the nearest million as needed.) d) How long after 1950 will the value of the painting be $3 billion? year(s) (Do not round until the final answer. Then round to the nearest year as needed.) (1) O dollar(s) per year. O year(s) per dollar.14. In 2011 a country's federal receipts (money taken in) totaled $2 25 trillion. In 2013, total federal receipts were $2 67 trillion. Assume that the growth of federal receipts, F, can be modeled by an exponential function and use 2011 as the base year (t = 0). Find the growth rate k to six decimal places, and write the exponential function F(t), for total receipts in trillions of dollars. b) Estimate total federal receipts in 2015. c) When will total federal receipts be $12 trillion? a) Find the growth rate k. K = (Do not round until the final answer. Then round to six decimal places as needed.) Write the exponential function F(t)- F(t) = b) Estimate total federal receipts in 2015. The total federal receipts in 2015 will be approximately $ trillion. (Use the answer from part (a) to find this answer. Round to two decimal places as needed.) c) When will total federal receipts be $12 trillion? The total federal receipts will be $12 trillion approximately years after 2011. (Use the answer from part (a) to find this answer. Round to one decimal place as needed.)15. Suppose that in 1667, a man bought a diamond for $37. Suppose that the man had instead put the $37 in the bank at 3% interest compounded continuously. What would that $37 have been worth in 2005? In 2005, the $37 would have been worth $ (Do not round until the final answer. Then round to the nearest dollar as needed.)16. a) The cost of first-class postage stamp was 74 in 1962 and 704 in 2010. This increase represents exponential growth. Write the function S for the cost of a stamp t years after 1962 (t = 0). b) What was the growth rate in the cost? c) Predict the cost of a first-class postage stamp in 2013, 2016, and 2019. d) The Forever Stamp is always valid as first-class postage on standard envelopes weighing 1 ounce or less, regardless of any subsequent increases in the first-class rate. An advertising firm spent $7000 on 10,000 first-class postage stamps in 2009. Knowing it will need 10,000 first-class stamps in each of the years 2010-2020, it decides at the beginning of 2010 to try to save money by spending $7000 on 10,000 Forever Stamps, but also buying enough of the stamps to cover the years 2011 through 2020. Assuming there is a postage increase in each of the years 2013, 2016, and 2019 to the cost predicted in part (c), how much money will the firm save by buying the stamps? a) Choose the correct answer below. O A. S(1) = 7ekt O B. S(t) = 0.05 8 71 O C. S(1) =7e Dost O D. S(t) = 0.05 g 701 b) The growth rate is approximately %. (Round to the nearest integer as needed.) c) The cost of a first-class postage stamp in 2013 is Use the answer from part (a) to find this answer. Round to the nearest integer as needed.) The cost of a first-class postage stamp in 2016 is Use the answer from part (a) to find this answer. Round to the nearest integer as needed.) The cost of a first-class postage stamp in 2019 is (Use the answer from part (a) to find this answer. Round to the nearest integer as needed.) d) The firm will save $ by buying the stamps at the beginning of 2010. Use the answers from part (c) to find this answer.)17. Suppose that a company introduces a new computer game in a city using television advertisements. Surveys show that P% of the target audience buy the game after x ads are broadcast, satisfying the equation below. Complete parts (a) through (d). 100 P(x) = - 1+48 g - 0.1x a) What percentage buy the game without seeing a TV ad (x = 0)? "Type an integer or a decimal rounded to the nearest tenth as needed.) b) What percentage buy the game after the ad is run 50 times? (Type an integer or a decimal rounded to the nearest tenth as needed.) c) Find the rate of change, P'(x)- P'(x) = d) Sketch a graph of the function. Choose the correct graph below. O A. O B. OC. OD. AP(I) APXI 100- 100- 100- 100- L" CO12. Between 2006 and 2016, the number of applications for patents, N, grew by about 4.6%% per year. That is, N'(1) = 0.046N(t). a) Find the function that satisfies this equation. Assume that t = 0 corresponds to 2006, when approximately 450,000 patent applications were received. bi Estimate the number of patent applications in 2021. Estimate the rate of change in the number of patent applications in 2021. a) N(t) = 450,000 / 0.04at b) The number of patent applications in 2021 will be 897,172 (Round to the nearest whole number as needed.) c) The rate of change in the number of patent applications in 2021 is about (1) - (Round to the nearest whole number as needed.) (1) O year(s) per application. O application(s) per year