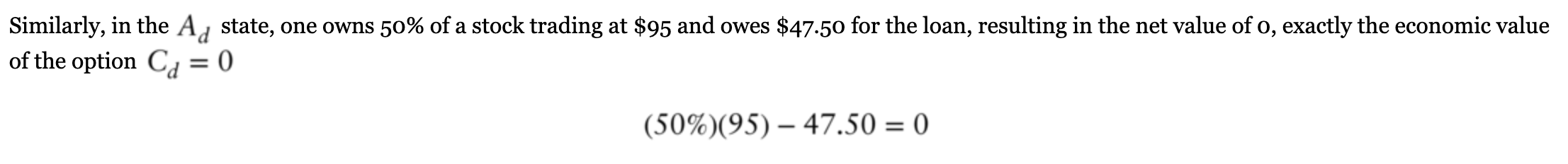Reference Example 2:

Reference Example 1:

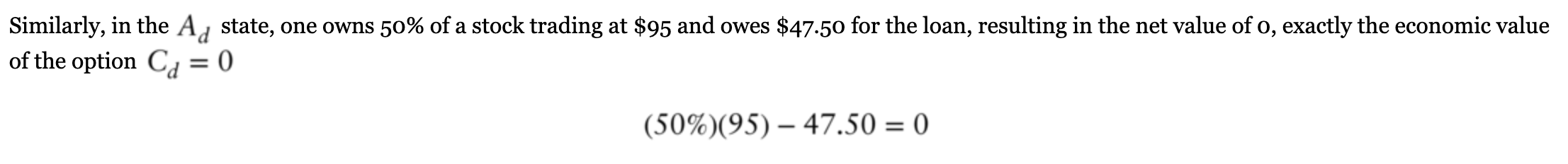
6. Using the same numerical values as in the 2-period binomial model in Example 2 a. Calculate today's price, P0, of a 6-month European put option with strike K=$100. b. Calculate today's value of a 6-month forward contract with purchase price K=$100. c. Verify that C0P0=VFA(0,T,K). Continuing with let us subdivide the time to expiration, T=6m, into two 3 -month intervals, and assume the stock's price evolves as shown in Figure 5:5. The replicating portfolio composition and the intermediate values of the option in Au,Ad are shown. Note that the replicating portfolio initially consists of Q0=62.44% of the stock funded in part by a 3-month loan of L0=59.35. Depending on whether we end up in Au or Ad in 3 months, the quantity and the loan size need to be dynamically adjusted. In the Au state, the required replicating portfolio is (Qu,Lu)=(87.5%,85.76) : one needs to borrow more to buy more of the stock. In the Ad state, the replicating portfolio is (Qd,Ld)=(12.5%,11.51) : one needs to reduce the position in the stock by selling it and using the proceeds to reduce the loan size. FIGURE 5:5 Two-period er Continuing with Example 2, note that the value of the portfolio coming into Au state is (62.44%)(103)+(59.35)e0.04/4=4.36 which is equal to the value of the portfolio after rebalancing (87.5%)(103)+(85.76)=4.36 Similarly, in the Ad state, the replicating portfolio is worth 0.62 before and after rebalancing: (62.44%)(97)+(59.35)e0.04/4=(12.5%)(97)+(11.51)=0.62 Let today's price of a stock be A0=$100, the 6-month continuously compounded interest rate r=4%, and assume that 6 months from today, the stock price can go up to Au=$105 or go down to Ad=$95. For a 6-month expiration (T=0.5) call option with strike K=$100, we have Cu=max(0,Au100)=5Cd=max(0,Ad100)=0 The replicating portfolio is computed as Q0=1059550=50%L0=e0.04/2(5(50%)(105))=46.56 and today's price of the call option is C0=(50%)(100)+(46.56)=3.44 The economic value of the call at expiration can replicated as follows: starting with $3.44 as the option premium, one can borrow $46.56 for 6 months at 4% to end up with $50 today, and use this to buy 50% of the stock trading at $100 per share. At expiration, the loan principal and interest are $46.56e0.04/2=$47.50. In the Au state, one owns 50% of a stock trading at $105 per share, and owes $47.50 for the loan, resulting in net value of $5, which is exactly the economic value of the option Cu=5. Similarly, in the Ad state, one owns 50% of a stock trading at $95 and owes $47.50 for the loan, resulting in the net value of o, exactly the economic value of the option Cd=0 (50%)(95)47.50=0