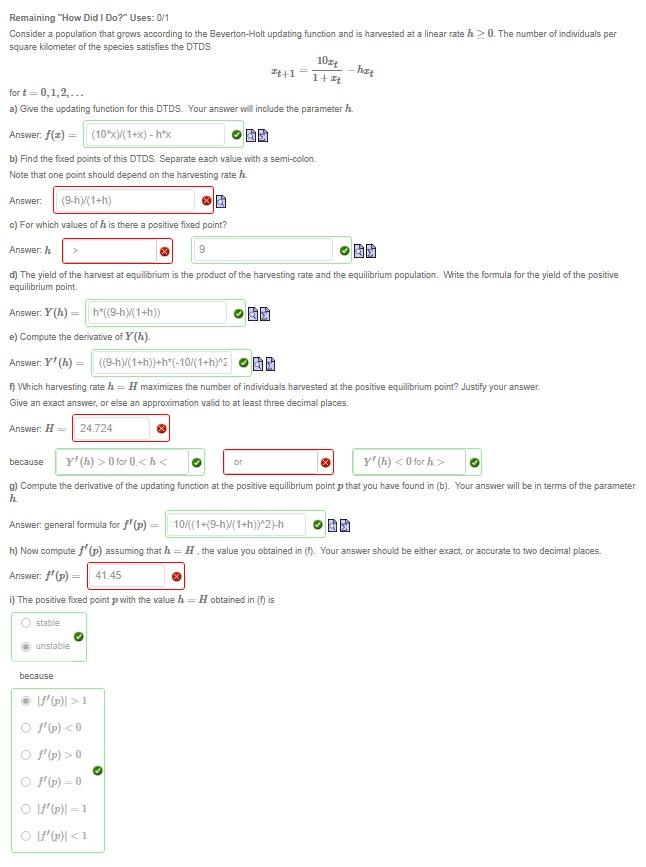
Remaining "How Did I Do?" Uses: 0/1 Consider a population that grows according to the Beverton-Holt updating function and is harvested at a linear rate h> 0. The number of individuals per square kilometer of the species satisfies the DTDS for t=0,1,2,... a) Give the updating function for this DTDS. Your answer will include the parameter h Answer: f(z) = (10*X)/(1+x)-h*x b) Find the fixed points of this DTDS. Separate each value with a semi-colon. Note that one point should depend on the harvesting rate h. Answer: (9-h)/(1+h) c) For which values of his there a positive fixed point? Answer: h 9 B d) The yield of the harvest at equilibrium is the product of the harvesting rate and the equilibrium population. Write the formula for the yield of the positive equilibrium point. Answer: Y(h) = h*((9-h)/(1+h)) e) Compute the derivative of Y(h). Answer: Y' (h) = ((9-h)/(1+h))+h*(-10/(1+h)^2 f) Which harvesting rate h H maximizes the number of individuals harvested at the positive equilibrium point? Justify your answer. Give an exact answer, or else an approximation valid to at least three decimal places. Answer: H = 24.724 unstable 24+1 because Y' (h) > 0 for () < h < O y! (h) < 0 for h> g) Compute the derivative of the updating function at the positive equilibrium point p that you have found in (b). Your answer will be in terms of the parameter h because 10z 1+z @f'(p)| >1 f' (p)