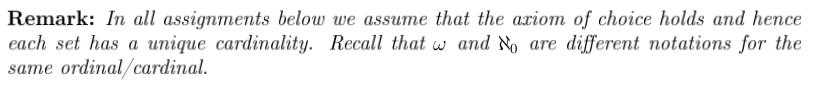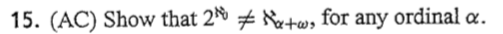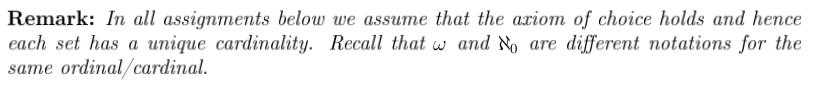
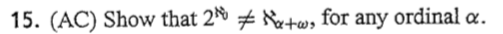
Remark: In all assignments below we assume that the axiom of choice holds and hence each set has a unique cardinality. Recall that w and No are different notations for the same ordinal cardinal. 15. (AC) Show that 2 + Xx+w, for any ordinal a. The aleph number system is used to identify the infinite cardinal numbers. The system is defined by transfinite recursion. As w is the first infinite cardinal, w will be the starting value of this recursion. We also need to define a "next cardinal function. By Corollary 9.1.9, we know that for each ordinal a, there is a cardinal that is "larger than a. Let S : On On be defined by (a) = the least cardinal k such that a Ek. Clearly, S is a class function. Consider the following definition by cases: w, if is the empty function; S[(y)), iff:yt + On for some ordinal y? y (9.2) sup IB). iff: On for some limit ordinal B; 0, if none of the above hold. Let $(y) be a formula that expresses (9.2). Hence, by Corollary 9.1.9, for every set f, there exists a unique y so that U.y). Thus, Theorem 8.2.4 implies that there exists a class function : On On such that if B = 0; N() = S(N(Y)), if B = y + for some ordinal y sup [B], if B is a limit ordinal. Note that S(R(Y)) = N(y + 1). Corollary 9.1.9 and Theorem 9.1.10 imply that N() is an infinite cardinal for every ordinal B. In addition, for each infinite cardinal K, there is an ordinal a such that (a) = * (see Theorem 9.1.11). (9.3) No. Exercise 15 and (9.3) imply that 8: On On is normal. For each ordinal B, we now let Ng = N(B). With this slight change in notation, (9.3) becomes if B = 0; Py+ if B = y + for some ordinal y; (9.4) sup[R: a B). if is a limit ordinal. The recursive definition (9.4) allows us to use the ordinals to identify all of the infinite cardinal numbers, in increasing order, as follows: NENE... EN +1 ... Nx+1... It follows that N = w. So, H is the first infinite cardinal. A is often referred to as aleph-naught. Since we X}, we see that ) (aleph-one) is the smallest uncountable cardinal Our next theorem verifies that the class function: On + On is increasing and "enumerates all of the cardinals. Theorem 9.1.11. For all ordinals a and B. ifa e B, then XE N. Moreover, for every infinite cardinal K, there is an ordinal a such that **. Lemma 9.2.14 (AC). R = 24. Remark: In all assignments below we assume that the axiom of choice holds and hence each set has a unique cardinality. Recall that w and No are different notations for the same ordinal cardinal. 15. (AC) Show that 2 + Xx+w, for any ordinal a. The aleph number system is used to identify the infinite cardinal numbers. The system is defined by transfinite recursion. As w is the first infinite cardinal, w will be the starting value of this recursion. We also need to define a "next cardinal function. By Corollary 9.1.9, we know that for each ordinal a, there is a cardinal that is "larger than a. Let S : On On be defined by (a) = the least cardinal k such that a Ek. Clearly, S is a class function. Consider the following definition by cases: w, if is the empty function; S[(y)), iff:yt + On for some ordinal y? y (9.2) sup IB). iff: On for some limit ordinal B; 0, if none of the above hold. Let $(y) be a formula that expresses (9.2). Hence, by Corollary 9.1.9, for every set f, there exists a unique y so that U.y). Thus, Theorem 8.2.4 implies that there exists a class function : On On such that if B = 0; N() = S(N(Y)), if B = y + for some ordinal y sup [B], if B is a limit ordinal. Note that S(R(Y)) = N(y + 1). Corollary 9.1.9 and Theorem 9.1.10 imply that N() is an infinite cardinal for every ordinal B. In addition, for each infinite cardinal K, there is an ordinal a such that (a) = * (see Theorem 9.1.11). (9.3) No. Exercise 15 and (9.3) imply that 8: On On is normal. For each ordinal B, we now let Ng = N(B). With this slight change in notation, (9.3) becomes if B = 0; Py+ if B = y + for some ordinal y; (9.4) sup[R: a B). if is a limit ordinal. The recursive definition (9.4) allows us to use the ordinals to identify all of the infinite cardinal numbers, in increasing order, as follows: NENE... EN +1 ... Nx+1... It follows that N = w. So, H is the first infinite cardinal. A is often referred to as aleph-naught. Since we X}, we see that ) (aleph-one) is the smallest uncountable cardinal Our next theorem verifies that the class function: On + On is increasing and "enumerates all of the cardinals. Theorem 9.1.11. For all ordinals a and B. ifa e B, then XE N. Moreover, for every infinite cardinal K, there is an ordinal a such that **. Lemma 9.2.14 (AC). R = 24