Round to four decimal places please

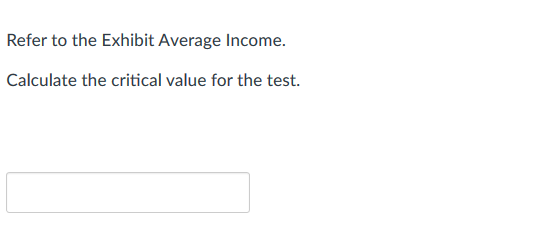
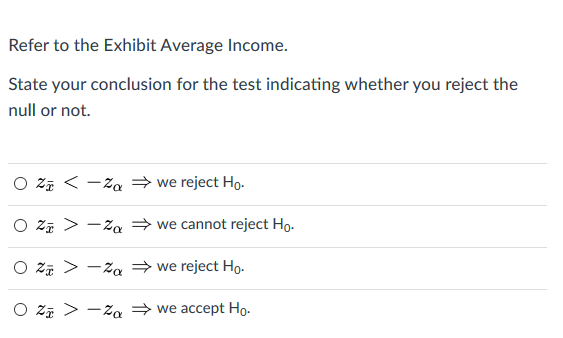
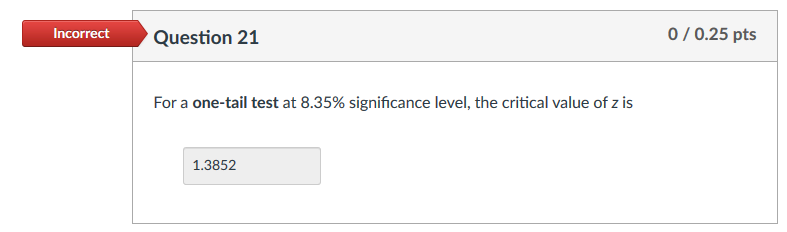
\f\fRefer to the Exhibit Average Income. We want to test to determine if there has been a decrease in the average yearly income of dentists (at the significance level 0.04). Construct the null and the alternative hypotheses for this test choosing the fields below: Ho: / [Select ] [ Select ] H1: H [ Select ] [ Select ]Refer to the Exhibit Average Income. Calculate the critical value for the test. Refer to the Exhibit Average Income. State your conclusion for the test indicating whether you reject the null or not. => we reject Ho- = we cannot reject Ho- O Z > -20 = we reject Ho- O ZX -20 = we accept Ho.Refer to the Exhibit Average Debt Load. Calculate the critical value for the test. Refer to the Exhibit Average Debt Load. State 1your conclusion for the test. 0 Zf2 we do not reject Ho. Therefore, there is not enough evidence to conclude that the average debt load of graduating students with a bachelor's degree is different from $1?,000. 0 Zaf2 we reject Ho. Therefore, there is enough evidence to conclude that the average debt load of graduating students with a bachelor's degree is different from $11000. O 3:2 .5 Zaf2 2? we reject Hu. Therefore. there is enough evidence to conclude that the average debt load of graduating students with a bachelor's degree is different from $11000. Refer to the Exhibit Average Debt Load. Calculate the p-value for the test. Exhibit: Average Debt Load. The Department of Education would like to check if the average debt load of graduating students with a bachelor's degree is different from $17,000. A random sample of 34 students had an average debt load of $18,200. It is believed that the population standard deviation for student debt load is $4,200. The significance level a is set to 0.02 for the hypothesis test. Round your solutions for this Exhibit to 4 decimal places.Exhibit: Average Income. The Bureau of Labor Statistics reported that the average yearly income of dentists in the year 2009 was $110,000. A sample of 34 dentists, which was taken in 2010, showed an average yearly income of $104,000. Assume the standard deviation of the population of dentists in 2010 is $21,000. Round your solutions for this Exhibit to 4 decimal places.Incorrect Question 21 0 / 0.25 pts For a one-tail test at 8.35% significance level, the critical value of z is 1.3852