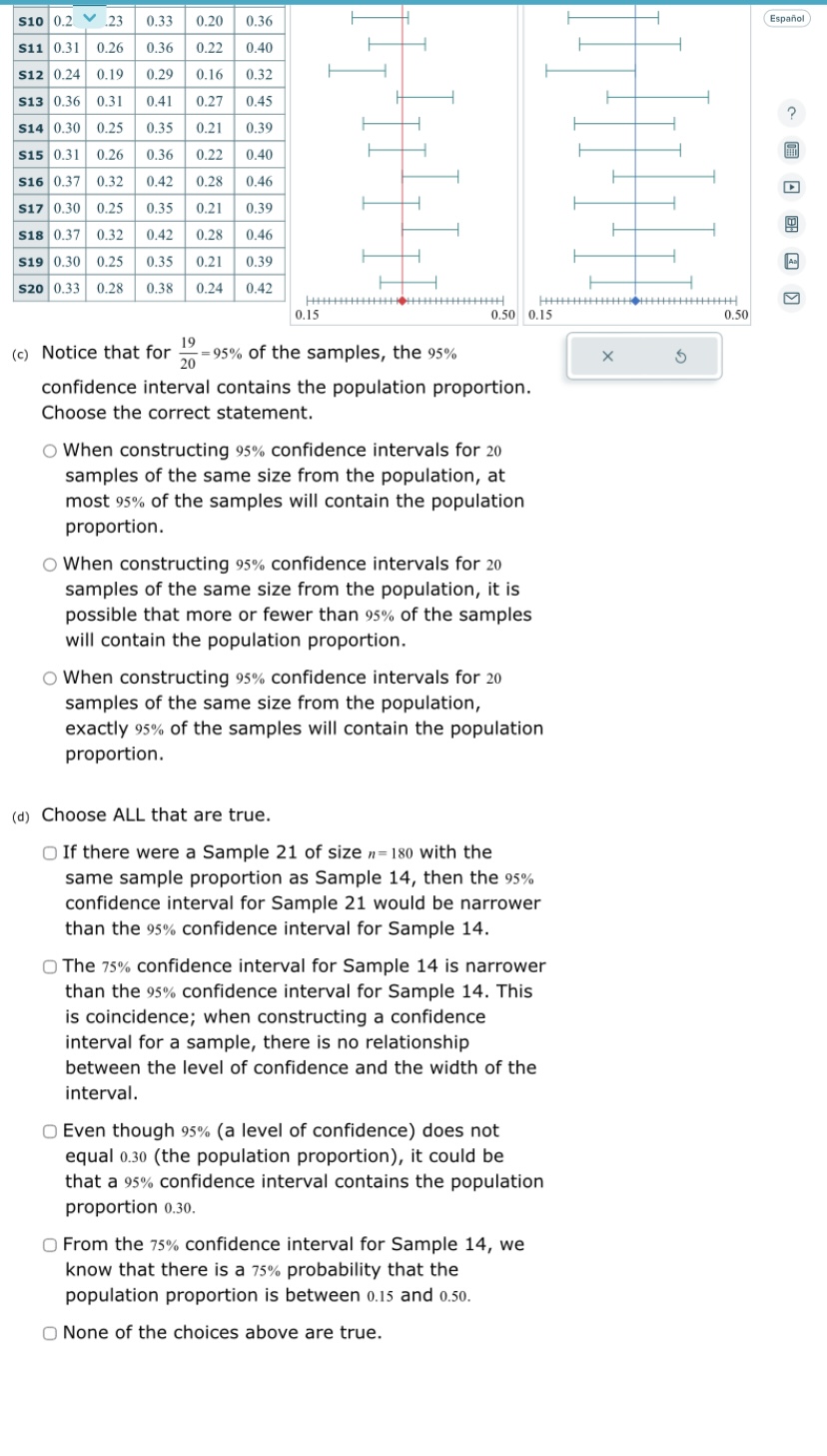
S1 0.3 99.4 101.2 98.9 101.7 515 99.6 98.7 100.5 98.2 101.0 S16 101.1 100.2 102.0 99.7 102.5 S17 100.4 99.5 101.3 99.0 101.8 S18 99.7 98.8 100.6 98.3 101.1 S19 99.8 98.9 100.7 98.4 101.2 S20 100.6 99.7 101.5 99.2 102.0 97.0 Espaol 104.0 97.0 104.0 (c) Notice that for 100% of the samples, the 95% 20 20 confidence interval contains the population mean. Choose the correct statement. When constructing 95% confidence intervals for 20 samples of the same size from the population, at least 95% of the samples will contain the population mean. When constructing 95% confidence intervals for 20 samples of the same size from the population, exactly 95% of the samples must contain the population mean. There must have been an error with the way our samples were chosen. When constructing 95% confidence intervals for 20 samples of the same size from the population, the percentage of the samples that contain the population mean should be close to 95%, but it may not be exactly 95%. (d) Choose ALL that are true. The 95% confidence interval for Sample 13 indicates that 95% of the Sample 13 data values are between 99.2 and 102.0. The 80% confidence interval for Sample 13 is narrower than the 95% confidence interval for Sample 13. This is coincidence; when constructing a confidence interval for a sample, there is no relationship between the level of confidence and the width of the interval. From the 80% confidence interval for Sample 13, we cannot say that there is an 80% probability that the population mean is between 99.7 and 101.5. If there were a Sample 21 of size n=36 taken from the same population as Sample 13, then the 95% confidence interval for Sample 21 would be wider than the 95% confidence interval for Sample 13. None of the choices above are true. A 2 > You have taken a random sample of size 2-18 from a normal population that has a population mean of 100 and a population standard deviation of a=3. Your sample, which is Sample 1 in the table below, has a mean of 98.8. (In the table, Sample 1 is written "S1", Sample 2 is written "S2", etc.) (a) Based on Sample 1, graph the 80% and 95% confidence intervals for the population mean. Use 1.282 for the critical value for the 80% confidence interval, and use 1.960 for the critical value for the 95% confidence interval. (If necessary, consult a list of formulas.) Enter the lower and upper limits on the graphs to show each confidence interval. Write your answers with one decimal place. For the points (and), enter the population mean, -100. 80% confidence interval 97.0 97.0 97.0 97.0 100.5 95% confidence interval 104.0 104.0 104.0 100.5 104.0 Espaol 1 > (b) Press the "Generate Samples" button below to simulate taking 19 more samples of size -18 from the population. Notice that the confidence intervals for these samples are drawn automatically. Then complete parts (c) and (d) below the table. 80% 80% 95% 95% lower upper lower upper limit limit limit limit ? ? 51 98.8 ? ? $2 100.4 99.5 101.3 99.0 101.8 53 100.4 99.5 101.3 99.0 101.8 S4 99.6 98.7 100.5 98.2 101.0 $5 99.5 98.6 100.4 98.1 100.9 56 99.8 98.9 100.7 98.4 101.2 $7 99.6 98.7 100.5 98.2 101.0 58 99.8 98.9 100.7 98.4 101.2 S9 100.3 99.4 101.2 98.9 101.7 510 996 98,7 1005 98.2 101.0 511 1012|100.3 | 102.1 $12 99.6 98.7 100.5 $13 100.6 99.7 S14 100.3 99.4 515 996 | 987 99.8 102.6 98.2 101.0 101.5 99.2 102.0 101.2 98.9 101.7 100.5 98.2 101.0 S16 101.1 100.2 102.0 99.7 102.5 101.3 99.0 101.8 S17 100.4 99.5 S18 99.7 98.8 100.6 98.3 101.1 $19 99.8 98.9 100.7 98.4 101.2 $20 100.6 99.7 101.5 99.2 102.0 80% confidence intervals 95% confidence intervals 97.0 104.0 97.0 (c) Notice that for 20 20 100% of the samples, the 95% confidence interval contains the population mean. Choose the correct statement. When constructing 95% confidence intervals for 20 samples of the same size from the population, at least 95% of the samples will contain the population mean. When constructing 95% confidence intervals for 20 samples of the same size from the population, exactly 95% of the samples must contain the population mean. There must have been an error with the way our samples were chosen. When constructing 95% confidence intervals for 20 samples of the same size from the population, the percentage of the samples that contain the population mean should be close to 95%, but it may not be exactly 95%. $10 0.2 23 0.33 0.20 0.36 S11 0.31 0.26 0.36 0.22 0.40 S12 0.24 0.19 0.29 0.16 0.32 S13 0.36 0.31 0.41 0.27 0.45 S14 0.30 0.25 0.35 0.21 0.39 S15 0.31 0.26 0.36 0.22 0.40 S16 0.37 0.32 0.42 0.28 0.46 S17 0.30 0.25 0.35 0.21 0.39 S18 0.37 0.32 0.42 0.28 0.46 S19 0.30 0.25 0.35 0.21 0.39 $20 0.33 0.28 0.38 0.24 0.42 H 0.15 H 0.50 0.15 19 (c) Notice that for 20 95% of the samples, the 95% confidence interval contains the population proportion. Choose the correct statement. When constructing 95% confidence intervals for 20 samples of the same size from the population, at most 95% of the samples will contain the population proportion. When constructing 95% confidence intervals for 20 samples of the same size from the population, it is possible that more or fewer than 95% of the samples will contain the population proportion. When constructing 95% confidence intervals for 20 samples of the same size from the population, exactly 95% of the samples will contain the population proportion. (d) Choose ALL that are true. If there were a Sample 21 of size n = 180 with the same sample proportion as Sample 14, then the 95% confidence interval for Sample 21 would be narrower than the 95% confidence interval for Sample 14. The 75% confidence interval for Sample 14 is narrower than the 95% confidence interval for Sample 14. This is coincidence; when constructing a confidence interval for a sample, there is no relationship between the level of confidence and the width of the interval. Even though 95% (a level of confidence) does not equal 0.30 (the population proportion), it could be that a 95% confidence interval contains the population proportion 0.30. From the 75% confidence interval for Sample 14, we know that there is a 75% probability that the population proportion is between 0.15 and 0.50. None of the choices above are true. G 0.50 Espaol CA 2 > You are Yooking at a population and are interested in the proportio papl that has a certain characteristic. Unknown to you, this population proportion is p=0.30. You have taken a random sample of size 110 from the population and found that the proportion of the sample that has the characteristic is p=0.27. Your sample is Sample 1 in the table below. (In the table, Sample 1 is written "S1", Sample 2 is written "S2", etc.) (a) Based on Sample 1, graph the 75% and 95% confidence intervals for the population proportion. Use 1.150 for the critical value for the 75% confidence interval, and use 1.960 for the critical value for the 95% confidence interval. (If necessary, consult a list of formulas.) Enter the lower and upper limits on the graphs to show each confidence interval. Write your answers with two decimal places. For the points (and), enter the population proportion, 0.30. 75% confidence interval 0.15 0.15 0.15 0.15 0.32 95% confidence interval 0.32 0.50 0.50 0.50 0.50 (b) Press the "Generate Samples" button below to simulate taking 19 more samples of size n=110 from the same population. Notice that the confidence intervals for these samples are drawn automatically. Then complete parts (c) and (d) below the table. 75% 75% 95% 95% lower upper lower upper limit limit limit limit 95% confidence intervals 75% confidence intervals $1 0.27 ? ? ? ? H S2 0.29 0.24 $3 0.29 0.24 S4 0.32 0.27 $5 0.40 0.35 $6 0.33 0.28 0.34 0.34 0.21 0.37 0.37 0.23 0.41 0.45 0.31 0.49 0.21 0.37 0.38 0.24 0.42 S7 0.29 0.24 0.34 0.21 0.37 S8 0.24 0.19 $9 0.31 0.26 $10 0.28 0.23 $11 0.31 0.26 0.29 0.16 0.32 0.36 0.22 0.40 $12 0.24 0.19 $13 0.36 0.31 $14 0.30 0.25 0.33 0.36 0.22 0.40 0.29 0.16 0.32 0.41 0.27 0.45 0.35 $15 0.31 0.26 0.36 S16 0.37 0.32 0.20 0.36 0.21 0.39 0.22 0.40 0.42 0.28 0.46 $17 0.30 0.25 0.35 0.21 0.39 S18 0.37 0.32 0.42 0.28 0.46 $19 0.30 0.25 0.35 0.21 0.39 $20 0.33 0.28 0.38 0.24 0.42 HH 0.15 CA > 0.50 0.15 0.50 19 (c) Notice that for 20-95% of the samples, the 95% confidence interval contains the population proportion. Choose the correct statement. When constr ting oz confidence intervale for sa