

SAMPLE


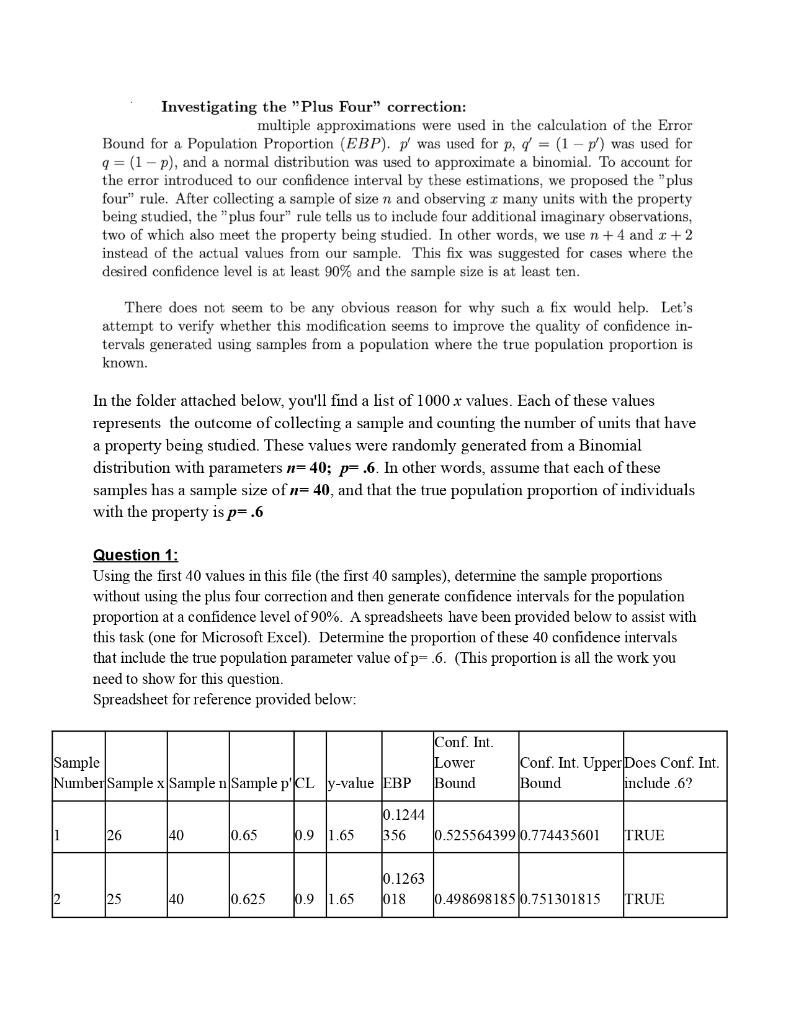
Investigating the "Plus Four" correction: multiple approximations were used in the calculation of the Error Bound for a Population Proportion (EBP). p/ was used for p, d = (1 - p') was used for q=(1-P), and a normal distribution was used to approximate a binomial. To account for the error introduced to our confidence interval by these estimations, we proposed the "plus four rule. After collecting a sample of size n and observing many units with the property being studied, the "plus four" rule tells us to include four additional imaginary observations, two of which also meet the property being studied. In other words, we use n +4 and 1+2 instead of the actual values from our sample. This fix was suggested for cases where the desired confidence level is at least 90% and the sample size is at least ten. There does not seem to be any obvious reason for why such a fix would help. Let's attempt to verify whether this modification seems to improve the quality of confidence in- tervals generated using samples from a population where the true population proportion is known. In the folder attached below, you'll find a list of 1000 x values. Each of these values represents the outcome of collecting a sample and counting the number of units that have a property being studied. These values were randomly generated from a Binomial distribution with parameters n=40; p= .6. In other words, assume that each of these samples has a sample size of n= 40, and that the true population proportion of individuals with the property is p= .6 Question 1: Using the first 40 values in this file (the first 40 samples), determine the sample proportions without using the plus four correction and then generate confidence intervals for the population proportion at a confidence level of 90%. A spreadsheets have been provided below to assist with this task (one for Microsoft Excel). Determine the proportion of these 40 confidence intervals that include the true population parameter value of p= .6. (This proportion is all the work you need to show for this question. Spreadsheet for reference provided below: Sample Conf. Int. Lower Bound Conf. Int. Upper Does Conf. Int. Bound include .6? Number Sample x Sample n Sample PCL y-value EBP 10.1244 356 11 26 40 0.65 0.9 1.65 0.52556439910.774435601 TRUE 10.1263 1018 2 25 140 10.625 0.9 1.65 10.4986981850.751301815 TRUE 3 23 40 10.575 0.1289 681 0.44603189 0.70396811 0.9 1.65 TRUE Question 1.1: Produce an image depicting these 40 confidence intervals using spreadsheet software, using the following guidelines: Your image should have one horizontal line at a height of p- .6, depicting the value of the true population parameter, For each con dence interval, draw a vertical line connecting the upper bound of the confidence interval to the lower bound of the con dence interval. Your plot should end up with 40 vertical bars. Please order them from left-to-right in the order that they occurred in the sample file below. Spreadsheet provided below shows a prototype for how this plot can be constructed. (I couldn't figure out how to get the software to draw lines connecting the points, so you might have to add them yourself either with image software or by hand) Sale Number 1 C.llower Blond 1 2 3 4 5 0.525944399 0.49185 4.11 b C.I.Upper und 0.774435601 0.151101615 0.70396811 0.9 08 02 06 0.4 Seks 0.1 O D 05 1 3.5 15 1 Sungle Number Question 2: Using the same first 40 values in this file (the first 40 samples), determine the sample proportions using the plus four correction and then generate confidence intervals for the population proportion at a confidence level of 90%. Determine the proportion of these 40 confidence intervals that include the true population parameter value of p=.6. (This proportion is all the work you need to show for this question) Question 2.1: Produce an image depicting the 40 confidence intervals from 2) using spreadsheet software, using the following guidelines: Your image should have one horizontal line at a height of p= 6, depicting the value of the true population parameter. . For each confidence interval, draw a vertical line connecting the upper bound of the confidence interval to the lower bound of the con dence interval. Your plot should end up with 40 vertical bars. Please order them from left-to-right. Question 3: In your own words, describe what the plots generated in 1.1) and 2.1) are showing Question 4: Repeat the analysis from 1), but use all 1000 samples in the file. What proportion of confidence intervals include the true population value? (This proportion is all you need to report Do not produce a plot.) Question 5: Repeat the analysis from 2), but use all 1000 samples in the file. What proportion of confidence intervals include the true population value? (This proportion is all you need to report Do not produce a plot.) Question 6: Discuss the results from Question 4 and Question 5. This study isn't sucient to prove anything definitive about the correction, but does it seem to be helping us achieve the desired behaviour from our confidence intervals? Or, at least, not harming the process? List goes from left to right, and next line left to right too 22 26 25 25 21 25 23 22 21 28 28 19 28 23 21 27 22 22 29 23 27 28 21 25 28 26 21 28 23 24 27 24 22 20 16 27 20 24 22 16 22 21 19 25 20 23 24 27 10 27 19 24 17 21 24 27 26 29 20 22 20 26 19 25 30 19 17 28 26 18 24 31 18 18 28 20 24 26 23 23 19 24 23 20 29 23 25 25 20 25 24 23 23 27 23 26 29 27 31 24 23 21 25 19 24 27 25 23 20 26 30 27 26 23 21 23 26 27 28 27 25 29 24 24 17 23 23 29 22 25 16 20 25 26 21 20 30 23 17 23 20 28 25 26 21 23 24 26 22 24 22 21 20 27 22 24 25 24 24 23 22 27 21 22 30 24 25 25 28 20 23 28 28 28 20 18 24 15 26 24 28 27 15 31 25 25 22 26 23 26 20 28 22 25 27 23 22 23 23 23 20 20 23 24 26 23 20 31 25 17 26 21 23 25 22 29 27 24 24 24 26 27 24 22 26 28 22 26 25 24 25 23 17 29 5 23 22 22 22 28 22 25 21 28 19 25 20 25 25 26 29 26 24 23 26 23 21 28 5 24 25 26 23 29 27 25 24 26 23 30 17 21 24 23 25 24 26 22 26 24 24 18 20 31 18 23 24 24 26 22 25 20 22 24 25 24 24 21 25 26 19 24 26 18 21 15 26 22 26 25 20 29 27 23 23 29 26 25 25 19 23 27 29 11 20 28 20 23 27 23 28 26 27 24 19 26 23 25 20 25 18 23 5 25 25 24 25 26 29 27 15 26 25 19 23 20 22 27 21 28 18 24 19 24 24 28 25 22 27 26 22 23 26 28 20 26 24 26 29 20 24 23 27 24 23 18 25 23 27 27 24 20 28 28 28 22 21 22 23 22 24 27 26 21 26 24 15 26 26 27 23 30 24 21 23 23 23 19 24 25 28 31 22 23 24 27 21 20 33 28 19 28 23 27 27 24 26 24 23 26 10 28 30 25 22 28 24 25 24 27 23 21 24 26 24 21 24 23 26 25 23 24 28 24 25 28 31 30 19 29 24 29 22 24 27 23 31 26 27 27 27 26 23 28 26 25 25 22 21 25 23 20 25 25 15 25 21 32 25 22 24 24 29 29 20 32 20 20 29 22 20 24 17 24 20 20 18 22 23 31 26 23 19 26 25 25 28 24 26 24 24 24 21 24 24 22 25 23 26 25 31 26 25 22 27 20 21 22 19 23 25 25 23 25 26 26 25 23 23 25 23 22 23 21 27 25 22 24 21 30 23 21 23 26 20 26 29 23 23 27 27 27 26 17 20 30 23 23 23 25 20 27 23 24 24 30 26 17 26 31 26 26 20 24 23 20 29 23 23 28 24 26 24 23 22 28 27 29 21 29 21 20 25 22 24 24 25 22 28 17 17 27 22 27 22 19 22 26 23 24 21 23 20 27 20 24 23 24 26 19 19 17 24 28 23 26 23 26 21 28 26 28 19 19 17 21 22 26 18 25 26 20 21 24 23 23 29 28 23 28 23 25 24 22 31 25 25 24 28 25 24 22 18 31 23 21 25 23 29 24 21 22 25 26 21 29 24 17 17 20 23 29 21 16 21 21 27 24 29 24 26 25 20 25 21 24 20 21 24 19 2) 28 27 26 24 27 24 22 25 20 22 29 16 27 24 22 24 24 22 26 19 26 23 26 21 23 27 23 28 29 22 24 19 27 28 28 21 26 24 25 23 22 23 31 26 24 21 24 24 26 2) 29 24 30 23 30 20 26) 24 25 26 27 24 24 24 25 24 26 26 25 21 25 22 25 21 26 21 22 23 25 24 20 22 20 21 32 25 24 26 29 24 24 17 23 25 25 23 27 25 23 23 24 24 2I 24 24 28 24 17 20 19 26 23 24 27 24 2) 25 24 20 23 33 25 21 26 23 28 19 21 22 27 21 18 23 23 20 17 27 19 32 25 19 26 28 22 23 23 22 26 27 28 23 19 24 16 21 23 20 29 23 26 26 26 24 22 30 29 24 26 22 16 26 26 23 26 28 25 25 23 17 22 25 22 26 22 22 28 25 26 28 23 23 22 25 26 25 27 29 21 27 29 23 25 25 27 24 22 30 24 23 29 29 22 21 27 28 25 26 27 24 28 18 22 15 24 27 19 25 22 23 23 22 20 25 23 23 27 23 22 28 21 19 29 28 20 27 25 20 28 21 24 21 21 28 28 25 24 23 25 19 26 25 22 27 23 25 24 28 Investigating the "Plus Four" correction: multiple approximations were used in the calculation of the Error Bound for a Population Proportion (EBP). p/ was used for p, d = (1 - p') was used for q=(1-P), and a normal distribution was used to approximate a binomial. To account for the error introduced to our confidence interval by these estimations, we proposed the "plus four rule. After collecting a sample of size n and observing many units with the property being studied, the "plus four" rule tells us to include four additional imaginary observations, two of which also meet the property being studied. In other words, we use n +4 and 1+2 instead of the actual values from our sample. This fix was suggested for cases where the desired confidence level is at least 90% and the sample size is at least ten. There does not seem to be any obvious reason for why such a fix would help. Let's attempt to verify whether this modification seems to improve the quality of confidence in- tervals generated using samples from a population where the true population proportion is known. In the folder attached below, you'll find a list of 1000 x values. Each of these values represents the outcome of collecting a sample and counting the number of units that have a property being studied. These values were randomly generated from a Binomial distribution with parameters n=40; p= .6. In other words, assume that each of these samples has a sample size of n= 40, and that the true population proportion of individuals with the property is p= .6 Question 1: Using the first 40 values in this file (the first 40 samples), determine the sample proportions without using the plus four correction and then generate confidence intervals for the population proportion at a confidence level of 90%. A spreadsheets have been provided below to assist with this task (one for Microsoft Excel). Determine the proportion of these 40 confidence intervals that include the true population parameter value of p= .6. (This proportion is all the work you need to show for this question. Spreadsheet for reference provided below: Sample Conf. Int. Lower Bound Conf. Int. Upper Does Conf. Int. Bound include .6? Number Sample x Sample n Sample PCL y-value EBP 10.1244 356 11 26 40 0.65 0.9 1.65 0.52556439910.774435601 TRUE 10.1263 1018 2 25 140 10.625 0.9 1.65 10.4986981850.751301815 TRUE 3 23 40 10.575 0.1289 681 0.44603189 0.70396811 0.9 1.65 TRUE Question 1.1: Produce an image depicting these 40 confidence intervals using spreadsheet software, using the following guidelines: Your image should have one horizontal line at a height of p- .6, depicting the value of the true population parameter, For each con dence interval, draw a vertical line connecting the upper bound of the confidence interval to the lower bound of the con dence interval. Your plot should end up with 40 vertical bars. Please order them from left-to-right in the order that they occurred in the sample file below. Spreadsheet provided below shows a prototype for how this plot can be constructed. (I couldn't figure out how to get the software to draw lines connecting the points, so you might have to add them yourself either with image software or by hand) Sale Number 1 C.llower Blond 1 2 3 4 5 0.525944399 0.49185 4.11 b C.I.Upper und 0.774435601 0.151101615 0.70396811 0.9 08 02 06 0.4 Seks 0.1 O D 05 1 3.5 15 1 Sungle Number Question 2: Using the same first 40 values in this file (the first 40 samples), determine the sample proportions using the plus four correction and then generate confidence intervals for the population proportion at a confidence level of 90%. Determine the proportion of these 40 confidence intervals that include the true population parameter value of p=.6. (This proportion is all the work you need to show for this question) Question 2.1: Produce an image depicting the 40 confidence intervals from 2) using spreadsheet software, using the following guidelines: Your image should have one horizontal line at a height of p= 6, depicting the value of the true population parameter. . For each confidence interval, draw a vertical line connecting the upper bound of the confidence interval to the lower bound of the con dence interval. Your plot should end up with 40 vertical bars. Please order them from left-to-right. Question 3: In your own words, describe what the plots generated in 1.1) and 2.1) are showing Question 4: Repeat the analysis from 1), but use all 1000 samples in the file. What proportion of confidence intervals include the true population value? (This proportion is all you need to report Do not produce a plot.) Question 5: Repeat the analysis from 2), but use all 1000 samples in the file. What proportion of confidence intervals include the true population value? (This proportion is all you need to report Do not produce a plot.) Question 6: Discuss the results from Question 4 and Question 5. This study isn't sucient to prove anything definitive about the correction, but does it seem to be helping us achieve the desired behaviour from our confidence intervals? Or, at least, not harming the process? List goes from left to right, and next line left to right too 22 26 25 25 21 25 23 22 21 28 28 19 28 23 21 27 22 22 29 23 27 28 21 25 28 26 21 28 23 24 27 24 22 20 16 27 20 24 22 16 22 21 19 25 20 23 24 27 10 27 19 24 17 21 24 27 26 29 20 22 20 26 19 25 30 19 17 28 26 18 24 31 18 18 28 20 24 26 23 23 19 24 23 20 29 23 25 25 20 25 24 23 23 27 23 26 29 27 31 24 23 21 25 19 24 27 25 23 20 26 30 27 26 23 21 23 26 27 28 27 25 29 24 24 17 23 23 29 22 25 16 20 25 26 21 20 30 23 17 23 20 28 25 26 21 23 24 26 22 24 22 21 20 27 22 24 25 24 24 23 22 27 21 22 30 24 25 25 28 20 23 28 28 28 20 18 24 15 26 24 28 27 15 31 25 25 22 26 23 26 20 28 22 25 27 23 22 23 23 23 20 20 23 24 26 23 20 31 25 17 26 21 23 25 22 29 27 24 24 24 26 27 24 22 26 28 22 26 25 24 25 23 17 29 5 23 22 22 22 28 22 25 21 28 19 25 20 25 25 26 29 26 24 23 26 23 21 28 5 24 25 26 23 29 27 25 24 26 23 30 17 21 24 23 25 24 26 22 26 24 24 18 20 31 18 23 24 24 26 22 25 20 22 24 25 24 24 21 25 26 19 24 26 18 21 15 26 22 26 25 20 29 27 23 23 29 26 25 25 19 23 27 29 11 20 28 20 23 27 23 28 26 27 24 19 26 23 25 20 25 18 23 5 25 25 24 25 26 29 27 15 26 25 19 23 20 22 27 21 28 18 24 19 24 24 28 25 22 27 26 22 23 26 28 20 26 24 26 29 20 24 23 27 24 23 18 25 23 27 27 24 20 28 28 28 22 21 22 23 22 24 27 26 21 26 24 15 26 26 27 23 30 24 21 23 23 23 19 24 25 28 31 22 23 24 27 21 20 33 28 19 28 23 27 27 24 26 24 23 26 10 28 30 25 22 28 24 25 24 27 23 21 24 26 24 21 24 23 26 25 23 24 28 24 25 28 31 30 19 29 24 29 22 24 27 23 31 26 27 27 27 26 23 28 26 25 25 22 21 25 23 20 25 25 15 25 21 32 25 22 24 24 29 29 20 32 20 20 29 22 20 24 17 24 20 20 18 22 23 31 26 23 19 26 25 25 28 24 26 24 24 24 21 24 24 22 25 23 26 25 31 26 25 22 27 20 21 22 19 23 25 25 23 25 26 26 25 23 23 25 23 22 23 21 27 25 22 24 21 30 23 21 23 26 20 26 29 23 23 27 27 27 26 17 20 30 23 23 23 25 20 27 23 24 24 30 26 17 26 31 26 26 20 24 23 20 29 23 23 28 24 26 24 23 22 28 27 29 21 29 21 20 25 22 24 24 25 22 28 17 17 27 22 27 22 19 22 26 23 24 21 23 20 27 20 24 23 24 26 19 19 17 24 28 23 26 23 26 21 28 26 28 19 19 17 21 22 26 18 25 26 20 21 24 23 23 29 28 23 28 23 25 24 22 31 25 25 24 28 25 24 22 18 31 23 21 25 23 29 24 21 22 25 26 21 29 24 17 17 20 23 29 21 16 21 21 27 24 29 24 26 25 20 25 21 24 20 21 24 19 2) 28 27 26 24 27 24 22 25 20 22 29 16 27 24 22 24 24 22 26 19 26 23 26 21 23 27 23 28 29 22 24 19 27 28 28 21 26 24 25 23 22 23 31 26 24 21 24 24 26 2) 29 24 30 23 30 20 26) 24 25 26 27 24 24 24 25 24 26 26 25 21 25 22 25 21 26 21 22 23 25 24 20 22 20 21 32 25 24 26 29 24 24 17 23 25 25 23 27 25 23 23 24 24 2I 24 24 28 24 17 20 19 26 23 24 27 24 2) 25 24 20 23 33 25 21 26 23 28 19 21 22 27 21 18 23 23 20 17 27 19 32 25 19 26 28 22 23 23 22 26 27 28 23 19 24 16 21 23 20 29 23 26 26 26 24 22 30 29 24 26 22 16 26 26 23 26 28 25 25 23 17 22 25 22 26 22 22 28 25 26 28 23 23 22 25 26 25 27 29 21 27 29 23 25 25 27 24 22 30 24 23 29 29 22 21 27 28 25 26 27 24 28 18 22 15 24 27 19 25 22 23 23 22 20 25 23 23 27 23 22 28 21 19 29 28 20 27 25 20 28 21 24 21 21 28 28 25 24 23 25 19 26 25 22 27 23 25 24 28











