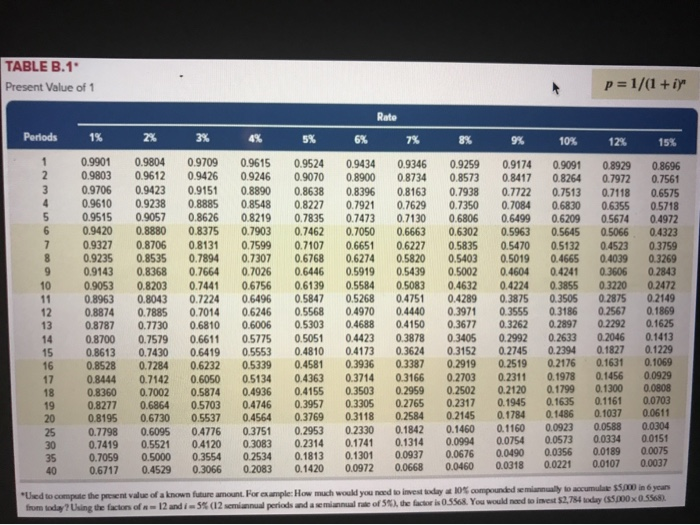
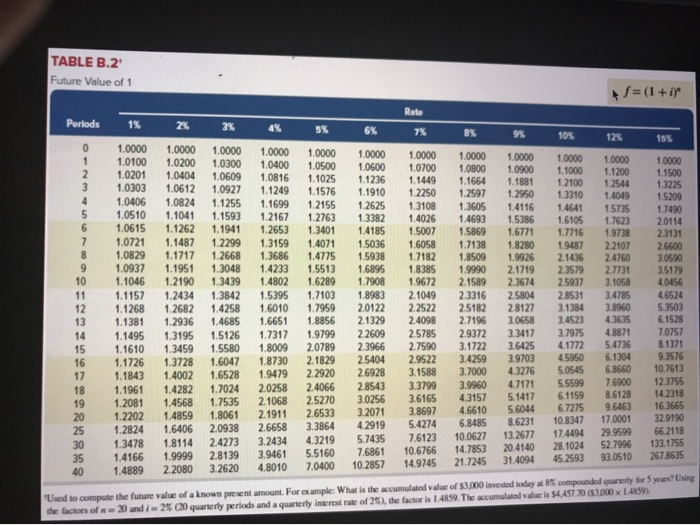
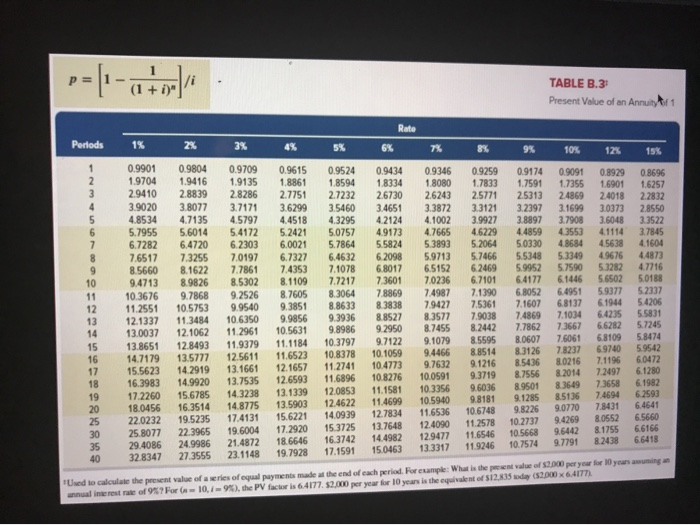
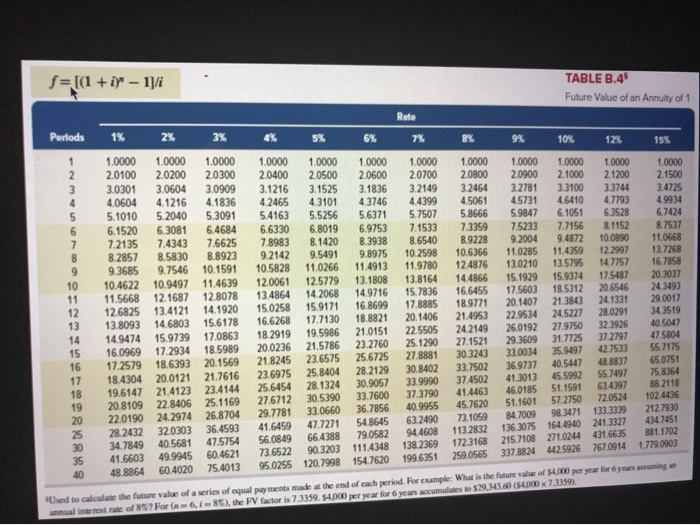
Saved Help Save & Exit Clara is setting up a retirement fund, and she plans on depositing $4,000 per year in an investment that will pay 7% annual interest. How long will it take her to reach her retirement goal of $55,266? (PV of $1. FV of $1. PVA of $1, and FVA of $1) (Use appropriate factor(s) from the tables provided.) 10 years To o o o 13.82 years .072 years 20 years 10 years 13.82 years .072 years 20 years 5.0 years TABLE B.1 Present Value of 1 p=1/(1+i)" Rate Periods 1% 2% 3% 4% 5% 6% 7% 8% 9% 10% 12% 15% 0.9901 0.9803 0.9706 0.9610 0.9515 0.9420 0.9327 0.9235 0.9143 0.9053 0.8963 0.8874 0.8787 0.8700 0.8613 0.8528 0.8444 0.8360 0.8277 0.8195 0.7798 0.7419 0.7059 0.6717 0.9804 0.9612 0.9423 0.9238 0.9057 0.8880 0.8706 0.8535 0.8368 0.8203 0.8043 0.7885 0.7730 0.7579 0.7430 0.7284 0.7142 0.7002 0.6864 0.6730 0.6095 0.5521 0.5000 0.4529 0.9709 0.9615 0.9426 0.9246 0.9151 0.8890 0.8885 0.8548 0.8626 0.8219 0.8375 0.7903 0.8131 0.7599 0.7894 0.7307 0.7664 0.7026 0.7441 0.6756 0.7224 0.6496 0.7014 0.6246 0.6810 0.6006 0.6611 0.5775 0.64190.5553 0.6232 0.5339 0.6050 0.5134 0.5874 0.4936 0.5703 0.4746 0.5537 0.4564 0.4776 0.3751 0.41200 .3083 0.3554 0.2534 0.3066 0.2083 0.9524 0.9434 0 .9346 0.9070 0.8900 0.8734 0.8638 0.8396 0.8163 0.8227 0.7921 0.7629 0.7835 0.7473 0.7130 0.7462 0.7050 0.6663 0.7107 0.6651 06227 0.6768 0.6274 0.5820 0.6446 0.5919 0.5439 0.6139 0.558405083 0.5847 0.5268 0.4751 0.5568 0.4970 0.4440 0.5303 0.4688 0.4150 0.4423 0.3878 0.48100.4173 0.3624 0.4581 0.3936 0.3387 0.4363 0.3714 0.3166 0.4155 0.3503 0.2959 0.3957 0.3305 0.2765 0.3769 0.3118 0.2584 0.2953 0.2330 0.1842 .2314 0.1741 0.1314 0.1813 0.1301 0 .0937 0.1420 0.0972 0.0668 0.9259 0.8573 0.7938 0.7350 0.6806 0.6302 0.5835 0.5403 0.5002 0.4632 0.4289 0.3971 0.3677 0.3405 0.3152 0.2919 0.2703 0.2502 0.2317 0.2145 0.1460 0.0994 0.0676 0.0460 0.9174 0.9091 0.8929 0.8417 0.8264 0.7972 0.7722 0.7513 0.7118 0.7084 0.6830 0.6355 0.6499 0.62090.5674 0.5963 0.5645 0.5066 0.5470 0.5132 0.4523 0.5019 0.4665 0.4039 0.4604 0.4241 0.3606 0.4224 0.3855 0.3220 0.3875 0.3505 0.2875 0.3555 0.3186 0.2567 0.3262 0.2897 0.2292 0.29920.2633 0.2046 0.2745 0.2394 0.1827 0.2519 0.2176 0.1631 0.2311 0.1978 0.1456 0.2120 0.1799 0.1300 0.1945 0.1635 0.1161 0.1784 0.1486 0.1037 0.1160 0.0923 0.0588 0.0754 0.0573 0.0334 0.0490 0.0356 0.0189 0.0318 0.0221 0.0107 0.8696 0.7561 0.6575 0.5718 0.4972 0.4323 0.3759 0.3269 0.2843 0.2472 0.2149 0.1869 0.1625 0.1413 0.1229 0.1069 0.0929 0.0808 0.0703 0.0611 0.0304 0.0151 0.0075 0.0037 0 40 "Used to compute the present value of a known future amount. For example: How much would you need to invested 10% compounded manually to accumulated in your from day Using the factors of 12 and 5% (12 semiannual periods and semiannual rate of the factor is 0.3568. You would need to invest 52,784. de (500x 0.3563 TABLE B.2 Future Value of 1 f=(1+i) Rate Periods 6% 7% 8% 9% 10% 12% 15% 1% 2% 3% 4% 5% 1.0000 1.000 1.0000 1.0000 10000 1.0100 1.0200 1.0300 1.0400 1.0500 1.0201 1.0404 1.0609 1,0816 1.1025 1.0303 1.0612 1.0927 1.1249 1.1576 1.0406 1.0824 1.1255 1.1699 1.2155 1.0510 1.1041 1.1593 1.2167 1.2763 1.0615 1.1262 1.1941 1.2653 1.3401 1.0721 1.1487 1.2299 1.3159 1.4071 1.0829 1.1717 1.2668 1.3686 1.4775 1.0937 1.1951 1.3048 1.42331.5513 1.1046 1.21901.3439 1.4802 1.6289 1.1157 1.2434 1.3842 1.5395 1.7103 1.1268 1.2682 1.4258 1.6010 1.7959 1.1381 1.2936 1.4685 1.6651 1.8856 1.1495 1.3195 1.5126 1.7317 1.9799 1.16101.3459 1.5580 1.8009 2.0789 1.1726 1.3728 1.6047 1.8730 2.1829 1.1843 1.4002 1.6528 1.9479 2.2920 1.1961 1.4282 1.7024 20258 2.4066 1.2081 1.4568 1.7535 2.1068 2.5270 1.2202 1.4859 1.8061 21911 2.1911 26533 1.2824 1.6406 2.0938 2.6658 3.3864 1.3478 1.8114 242733.2434 4.3219 1.4166 1.9999 2.81393.9461 5.5160 .4889 2.2080 3.2620 4.8010 7.0400 10000 10000 10000 1.0600 1.0700 1.0800 1.1236 1.1449 1.1910 1.2250 1.2597 1.2625 1.3108 1.3605 1.3382 1.4026 1.4693 1.4185 15007 1.5036 1.6058 1.7138 1.5938 1.7182 1.8509 1.6895 1.8385 1.9990 1.7908 1.9672 2.1589 1.8983 2.1049 2.3316 2 0122 2.2522 2.5182 2.1329 2.4098 2.7196 2.2609 2.5785 2.9372 2.3966 2.7590 3.1722 2.5404 2.9522 3.4259 2.6928 3.1588 3.7000 28543 3.3799 3.9960 3.0256 3.61654 .3157 3.2071 3.8697 4.6610 4.2919 5.4274 6.8485 5.7435 7 .6123 10.0627 7.686110.6766 14.7853 10.2857 14.9745 21.7245 10000 10000 10000 1.0900 1.1000 1.1200 1.1881 1.2100 1.2544 1.2950 1.3310 1.4116 1.4641 1.5735 1.5386 1.6105 1.7623 1.6771 1.7716 1.9738 1.9487 2.2107 1.9926 2.1436 2.4760 2.1719 2.3579 2.7731 2.3674 2.5937 3.1058 2.5804 2.8531 3.4785 2.8127 3.1384 3.8960 3.0658 3.4523 4 .3635 3.3417 3.7975 4.8871 3.6425 4.1772 5.4736 3.9703 5950 6.1304 43276 5.0545 6.8660 4.7171 5.5599 7.6900 5.14176.11598.6128 5.6044 6.7275 9.6463 8.6231 10.8347 17.0001 13.2677 17.4494 29.9599 20.4140 28.1024 52.7996 31.4094 45.259393.0510 10000 1.1500 13225 1.5209 1.7490 20114 2.3131 26600 3.0590 3.5179 4.0456 4.6524 53503 6.1528 7.0757 8.1371 9.3576 10.7613 12.3755 14.2318 1 6.3665 32.9190 66.2118 133.1755 267.8635 35 40 1 n g "Used to compute the future value of a known presentamount. For example: What is the accumulated value of $1,000 invested today at 8 compounded quarterly for you the factors of 20 and 2 (20 quarterly periods and a quarterly interest rate of 25).the factor is 1 4859. The accumulated value is $4.457.70 500 X LARSON p= [1-a tist] TABLE B.3: Present Value of an Annuityti Periods 1% 2% 3% 4% 6% 7 10 0.9901 1.9704 2.9410 3.9020 4.8534 5.7955 6.7282 7.6517 8.5660 9.4713 10.3676 11.2551 12.1337 13.0037 13.8651 14.7179 15.5623 16.3983 17.2260 18 0456 22.0232 25.8077 29.4086 328347 12 0.9804 0.9709 0.9615 1.9416 1.9135 1.8861 2.8839 2.8286 2.7751 3.8077 3.7171 3.6299 4.7135 4.5797 4.4518 5.6014 5.4172 5.2421 6.4720 6.2303 6.0021 7.3255 7,0197 6.7327 8.1622 7.7861 7.4353 8.9826 8.5302 8.1109 9.7868 9.2526 8.7605 10.5753 9.9540 9.3851 11.3484 10.6350 9.9856 12.1062 11.2961 10.5631 12.8493 11.9379 11.1184 13.5777 12.5611 11.6523 14.291913.1661 12.1657 14.9920 13.7535 12.6593 15.6785 14.3238 13.1339 16 2514 14.8775 13 5903 19.5235 17.4131 15.6221 22.3965 19.600417.2920 24.9986 21.4872 18.6646 27.3555 23.1148 19.7928 0.9524 1.8594 2.7232 3.5460 4.3295 5.0757 5.7864 6.4632 7.1078 7.7217 8.3064 8.8633 9.3936 9.8986 10.3797 10.8378 11.2741 11.6896 12.0853 12 4622 14.0939 15 3725 16.3742 17.1591 0.9434 18334 2.6730 3.4651 42124 4.9173 5.5824 6.2098 6.8017 7.3601 78869 8.3838 8.8527 9.2950 9.7122 10.1059 10.4773 10.8276 11.1581 11.4699 12.7834 13.7648 14.4982 15.0463 9% 10% 12% 15% 0.9174 0.9091 0.8929 0.8696 1.7591 1.7355 1.6901 1.6257 2.53132486924018 2.2832 3.2397 3.16993.0373 2.8550 3.8897 3.7908 3.6048 3.3522 4.48594.3553 4.1114 3.7845 5.0330 4.8684 4.5638 4.1604 5.5348 5.33494.9676 4.4873 5.9952 5.7590 53282 47716 6.4177 6.1446 5.65025.0188 6805264951 59377 5.2337 7.1607 6.8137 6.1944 5.4206 7.48697.1034 6.4235 5.5831 7.786273667 6.62825.7245 8.0607 7.6061 6.81095.8474 8.3126 78237 69740 59542 8.5436 8.0216 7.1196 6.0472 8.7556 8.2014 7.2497 6.1280 8.9501 836497.3658 6.1982 9.1285 85136 7.4694 6.2593 9.8226 9.07707.8431 6.4641 10.2737 9.42698.0552 6.5660 10.5668 9.64428.1755 6.6166 10.7574 9.7791 8.2438 6.6418 0 .9346 0.9259 1 8080 1.7833 2.6243 2.5771 3.3872 3.3121 4.1002 3.9927 4.7665 4.6229 53893 5.2064 5.9713 5.7466 6.5152 6.2469 7.0236 6.7101 7.4987 7.1390 7.9427 7.5361 8.3577 7.9038 8.74558.2442 9.1079 8.5595 9 4466 88514 9.7632 9 .1216 10.0591 9.3719 10.3356 9.6036 1 05940 9.8181 11.6536 10.6748 12.4090 11.2578 12.9477 11.6546 13.3317 11.9246 Used to calculate the present value of a series of equal payments made at the end of each period. For example: What is the pewn value of $2.000 per year for 10 years wming an annual interest rate of 97 For 10, 1 9 ), the PV factor is 6,4177.52,000 per year for 10 years in the equivalent of 512,835 day (52.000 x 64ITT f=[(1 + i)" - 13/1 100890 11.0668 TABLE B.4 Future Value of an Annuity of 1 Rato Periods 23 3% 4% 5% 6% 7% 8% 9% 10% 12% 15% 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 2.0100 1.0000 1.0000 2.0200 1.0000 2.0300 1.000 2.0400 1.000 2.0500 1.0000 2.0600 2.0700 2.0800 3.0301 2.0900 2.1000 3.0604 2.1200 3.0909 3.1216 2.1500 3.15253.1836 3.21493.2464 4.0604 3.2781 3.3100 3.3744 4.1216 4.1836 3.4725 4.2465 4.3101 4.3746 4.4399 4.5061 4.5731 4.64104.7793 5.1010 5.2040 4.9934 5.3091 5 .4163 5.5256 5.6371 5.7507 5.8666 5.98476.1051 6.3528 6.7424 6.1520 6.3081 6.4684 6.6330 6.80196.9753 7.1533 7.33597.52337.7156 8.11528.7537 7.2135 7.4343 7.6625 7 .89838.1420 8.3938 8.6540 8.9228 9.2004 9.4872 10.0890 8.2857 8.5830 8.8923 9 .2142 9.5491 9.8975 10.2598 10.6366 11.0285 11.4359 12 2997 13.7268 9.3685 9.7546 10.1591 10.5828 11.0266 11.491311.9780 12.4876 13.0210 13.5795 14.7757 16.7858 10.4622 10.9497 11.4639 12.0061 12.5779 13.1808 13.8164 14.4866 15.1929 15.9374 17.5487 20.3037 11.5668 12.1687 12.8078 13.4864 14.2068 14.9716 15.7836 16.6455 17.560318.5312 20.6546 24.3493 12.6825 13.4121 14.1920 15.0258 15.9171 16,8699 17.8885 18.9771 20.1407 21.3843 24.1331 29.0017 13.8093 14.6803 15.6178 16.6268 17.7130 18.8821 20.1406 21.49532 2.9534 24.5227 28.0291 34.3519 14.9474 15.9739 17.0863 18.2919 19.5986 21.0151 22.5505 24.2149 26.0192 27.9750 32.3926 40.5047 16.0969 17.2934 18.5989 20.0236 21.5786 23.2760 25.1290 27.152129.360931.7725 37.2797 47.5804 17.2579 18.6393 20.1569 25.6725 27.8881 30.3243 33.0034 35.9497 42.7533 55.7175 18.4304 20.0121 21.7616 23.6975 25.8404 28.212930.8402 33.7502 650751 36.9737 40.5447 48.8837 18 19.6147 21.4123 75.8364 55.7497 28.1324 25.6454 23.4144 30.9057 37.450241.301345.5992 33.9990 20.8109 22.8406 33.7600 30.5390 25.116927.6712 37.3790 88 2118 63.4397 41.4463 46.0185 51.1591 720524 22.0190 24.2974 26.8704 102.4436 72.0524 33,0660 29.7781 57.2750 40.9955 36.7856 51.1601 45.7620 212.7930 63 2490 47.7271 133.3339 73.1059 84.700998.3471 54.8645 41.6459 36.4593 28.2432320303 25 434.7451 136,3075 164.4940 2413327 113.2832 79.058294.4608 34.7849 40.5681 56.084966.4388 47.5754 41.6603 215.7108 271.02444316635881.1702 90.3203 138.2369172.3168 73.6522 49.994560.4621 1114348 1.779.0903 442.5926767.0914 259,0565337.8824 154.7620 120.7998 199.6351 40 75.401395.0255 60.4020 48 8864 of S460 per year for your the end of each period. For example: What is the future Used to calculate the future value of a series of equal payments made annual interest rate of 8? For 6,1 8%), the FV factor is 7.3359. 54.000 per year for 6 years accumulates to $29,343 60 54.000 x 73359 12 15 16