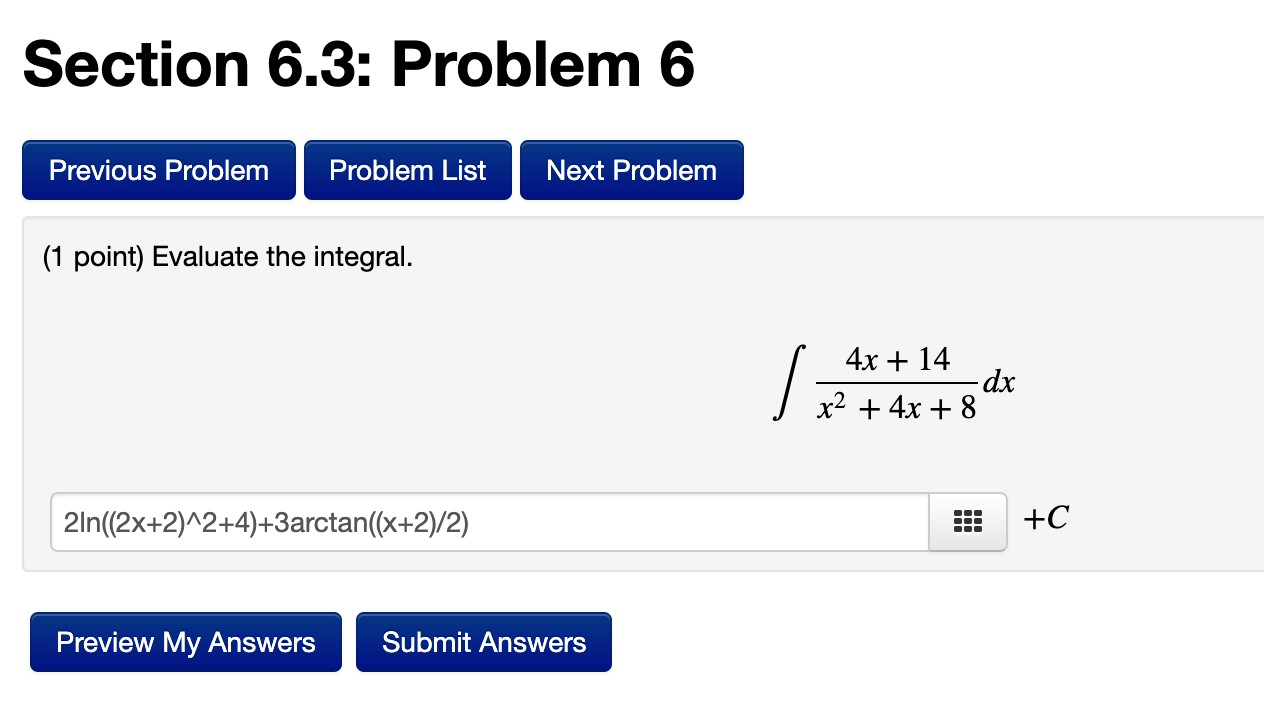
Question: Section 6.3: Problem 6 Previous Problem Problem List Next Problem (1 point) Evaluate the integral. 4x + 14 x2 + 4x + 8 dx 2In((2x+2)^2+4)+3arctan((x+2)/2)

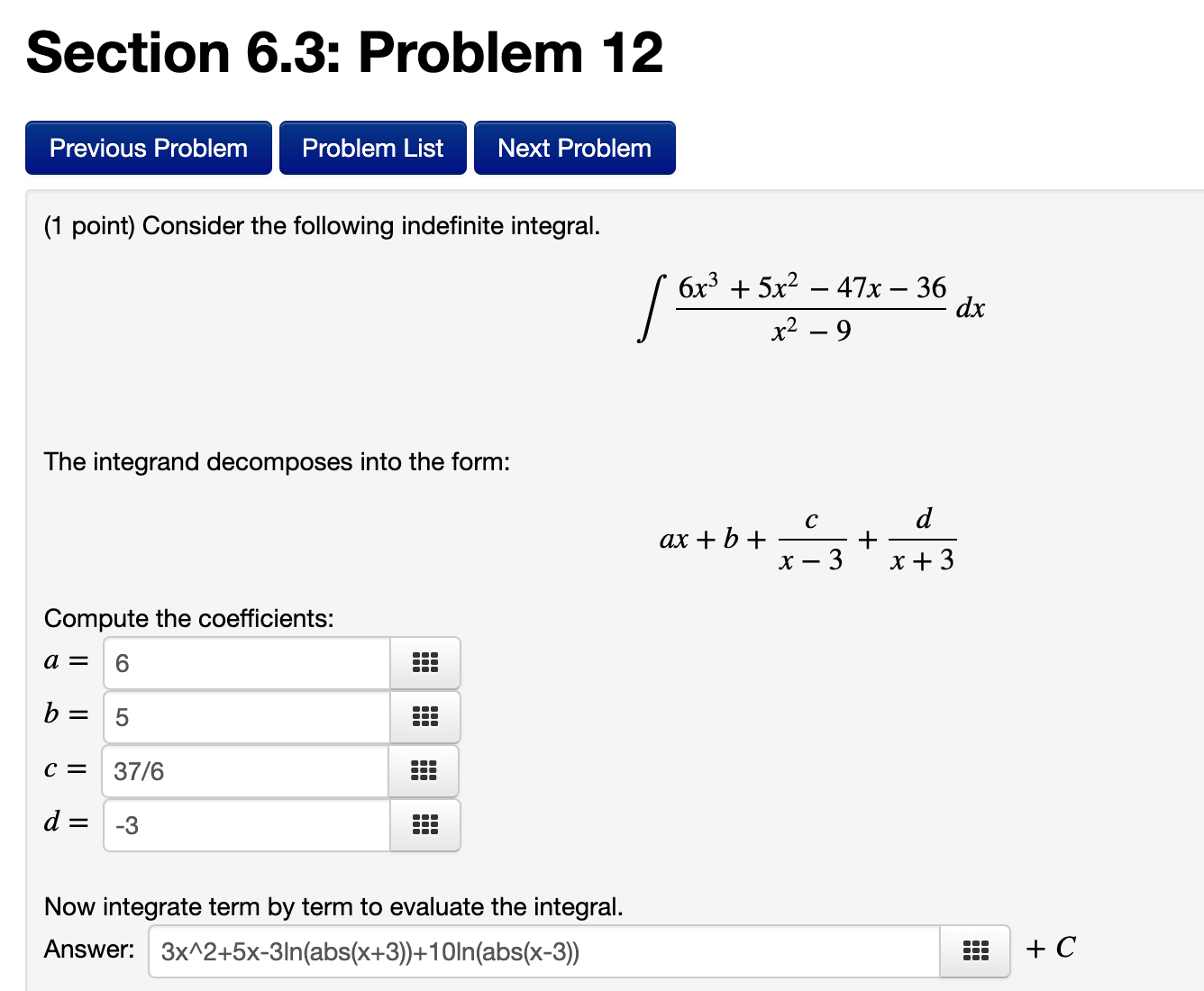
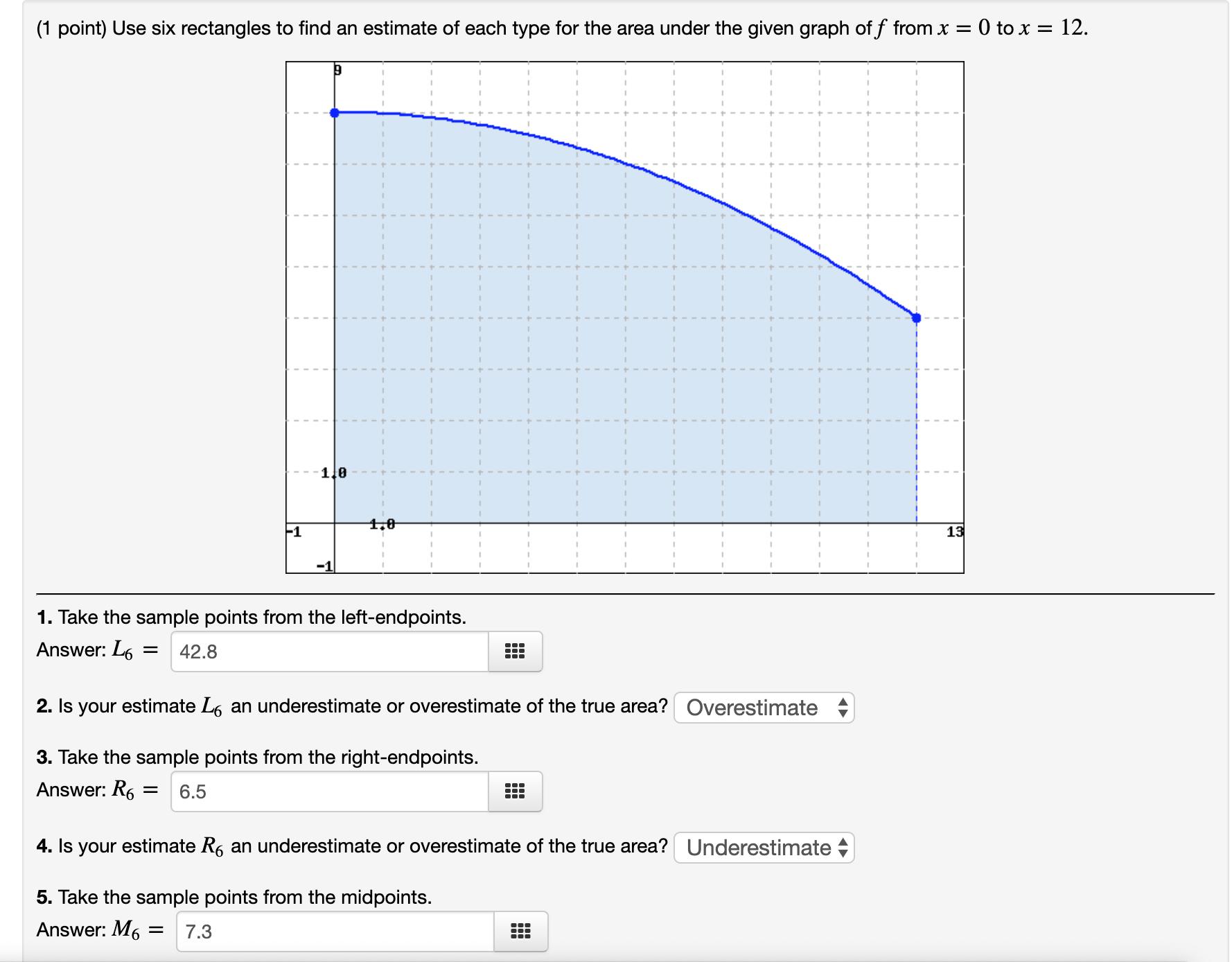
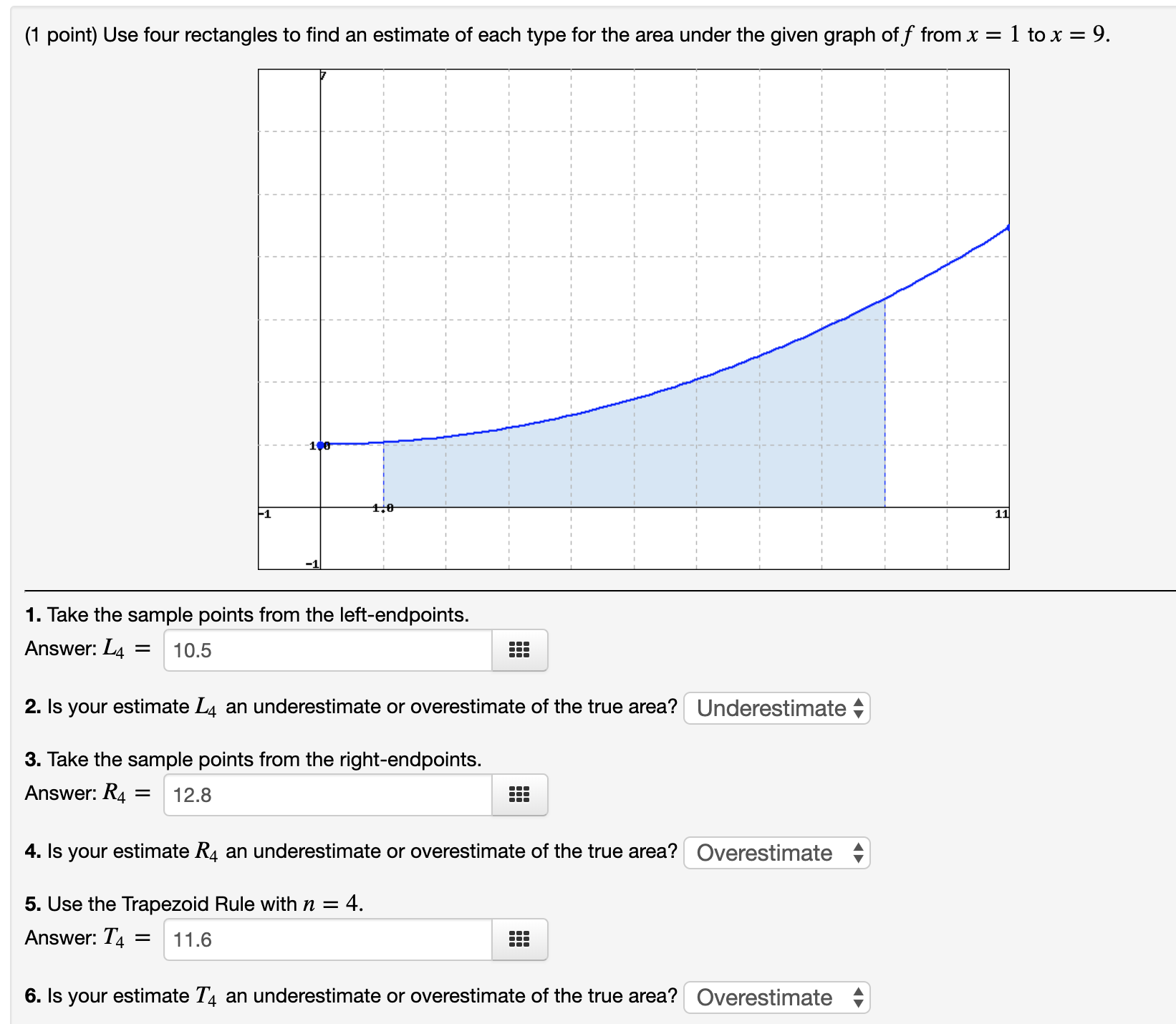
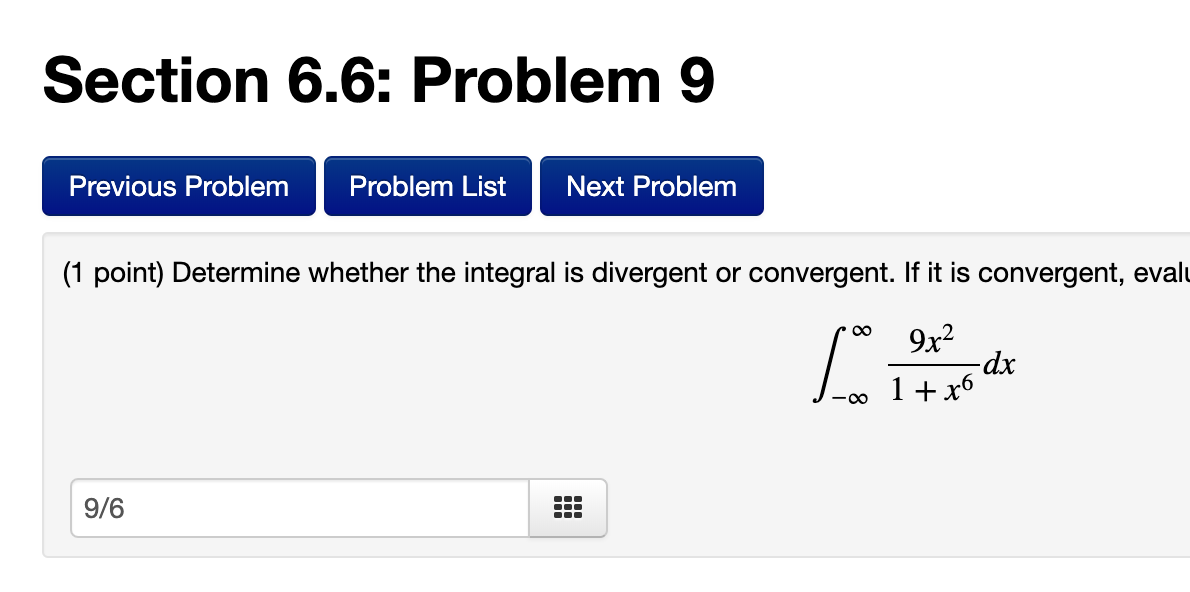
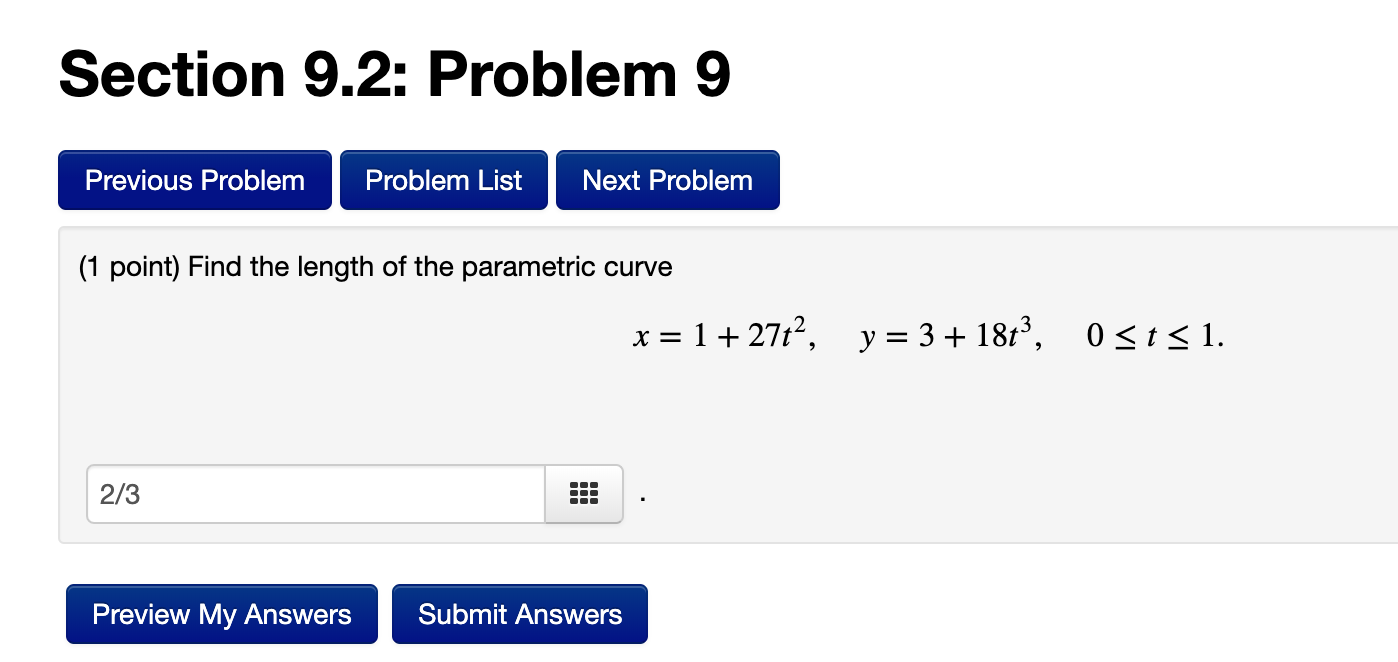
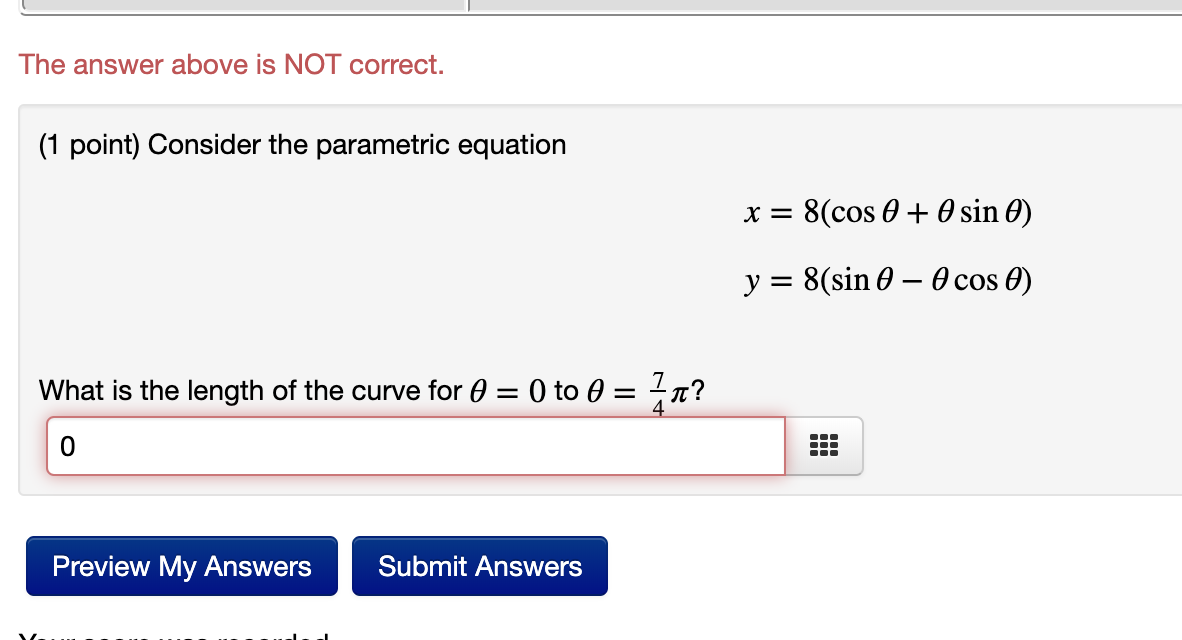
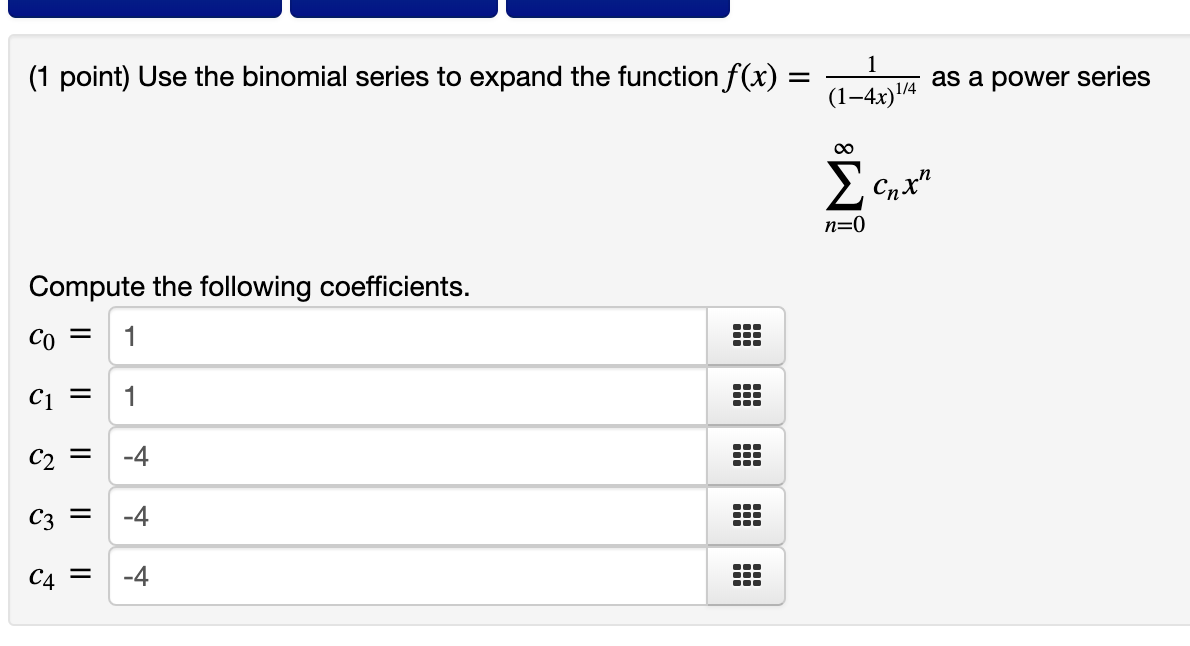



Section 6.3: Problem 6 Previous Problem Problem List Next Problem (1 point) Evaluate the integral. 4x + 14 x2 + 4x + 8 dx 2In((2x+2)^2+4)+3arctan((x+2)/2) +C Preview My Answers Submit AnswersSection 6.3: Problem 8 Previous Problem Problem List Next Problem (1 point) Evaluate the integral. -30ex - 120 e2x + 11ex + 24 dx Answer = +C Preview My Answers Submit Answers You have attempted this problem 0 times.Section 6.3: Problem 12 Previous Problem Problem List Next Problem (1 point) Consider the following indefinite integral. 6x3 +5x2 - 47x - 36 x2 - 9 dx The integrand decomposes into the form: ax+b+ C d + x - 3 x+3 Compute the coefficients: a= 6 b 5 CE 37/6 d = -3 Now integrate term by term to evaluate the integral. Answer: 3x^2+5x-3In(abs(x+3))+10In(abs(x-3)) + C(1 point) Use six rectangles to find an estimate of each type for the area under the given graph of f from x = 0 to x = 12. 1. Take the sample points from the left-endpoints. Answer: La = 42.8 555 2. Is your estimate L5 an underestimate or overestimate of the true area? overestimate 3 3. Take the sample points from the right-endpoints. Answer: R5 = 6.5 555 4. Is your estimate R6 an underestimate or overestimate of the true area? Underestimate c 5. Take the sample points from the midpoints. Answer: M5 = 7.3 =:: (1 point) Use four rectangles to find an estimate of each type for the area under the given graph of f from x = 1 to x = 9. 1. Take the sample points from the left-endpoints. Answer:L4 = 10.5 555 2. Is your estimate L4 an underestimate or overestimate of the true area? underestimate 3. Take the sample points from the right-endpoints. Answer: R4 = 12.3 ::: 4. Is your estimate R4 an underestimate or overestimate of the true area? overestimate ' 5. Use the Trapezoid Rule with n = 4. Answer: T4 = 11.5 ::: 6. Is your estimate T4 an underestimate or overestimate of the true area? overestimate ' Section 6.6: Problem 9 Previous Problem Problem List Next Problem (1 point) Determine whether the integral is divergent or convergent. If it is convergent, eval 9x2 1 + x6 dx 9/6Section 9.2: Problem 9 (1 point) Find the length of the parametric curve x=1+27t2, 2/3 555 Preview My Answers Submit Answers 't I The answer above is NOT correct. (1 point) Consider the parametric equation x = 8(cosf9+ 49st y = 8(sin6 60039) What is the length of the curve for a = 0 to 9 = at? Preview My Answers Submit Answers \\l_____ _ _____ _____ .__ __.__I__I 1 (141)\"4 (1 point) Use the binomial series to expand the function f(x) = as a power series 00 Z cnx" n=0 Compute the following coefficients. co = 1 555 C1 = 1 E (32 = -4 c3 = -4 49 II I A III III III (1 point) Evaluate (3'3\"3 1 + 3x3 2x x>0 8x9 Hint: Using power series. 1/(16*3!) 555 Preview My Answers Submit Answers (1 point) a) Consider the function arctan(x2). Write a partial sum for the power series which represents this function consisting of the first 4 nonzero terms. For example, if the series were _n= 3" x2 , you would write 1 + 3x2 + 32 x4 + 35x. Also indicate the radius of convergence. Partial Sum: -X12 Radius of Convergence: b) Use part a) to write the partial sum for the power series which represents / arctan(x2 )dx. Write the first 4 nonzero terms. Also indicate the radius of convergence. Partial Sum: Radius of Convergence: c) Use part b) to approximate the integral , arctan(x2 )dx.\fSection 8.6: Problem 10 (1 point) Consider the function arctan(x/ 15). Write a partial sum for the power series which represents this function consisting of the first 5 nonzero terms. For example, if the series were 22:0 3nx2\
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


