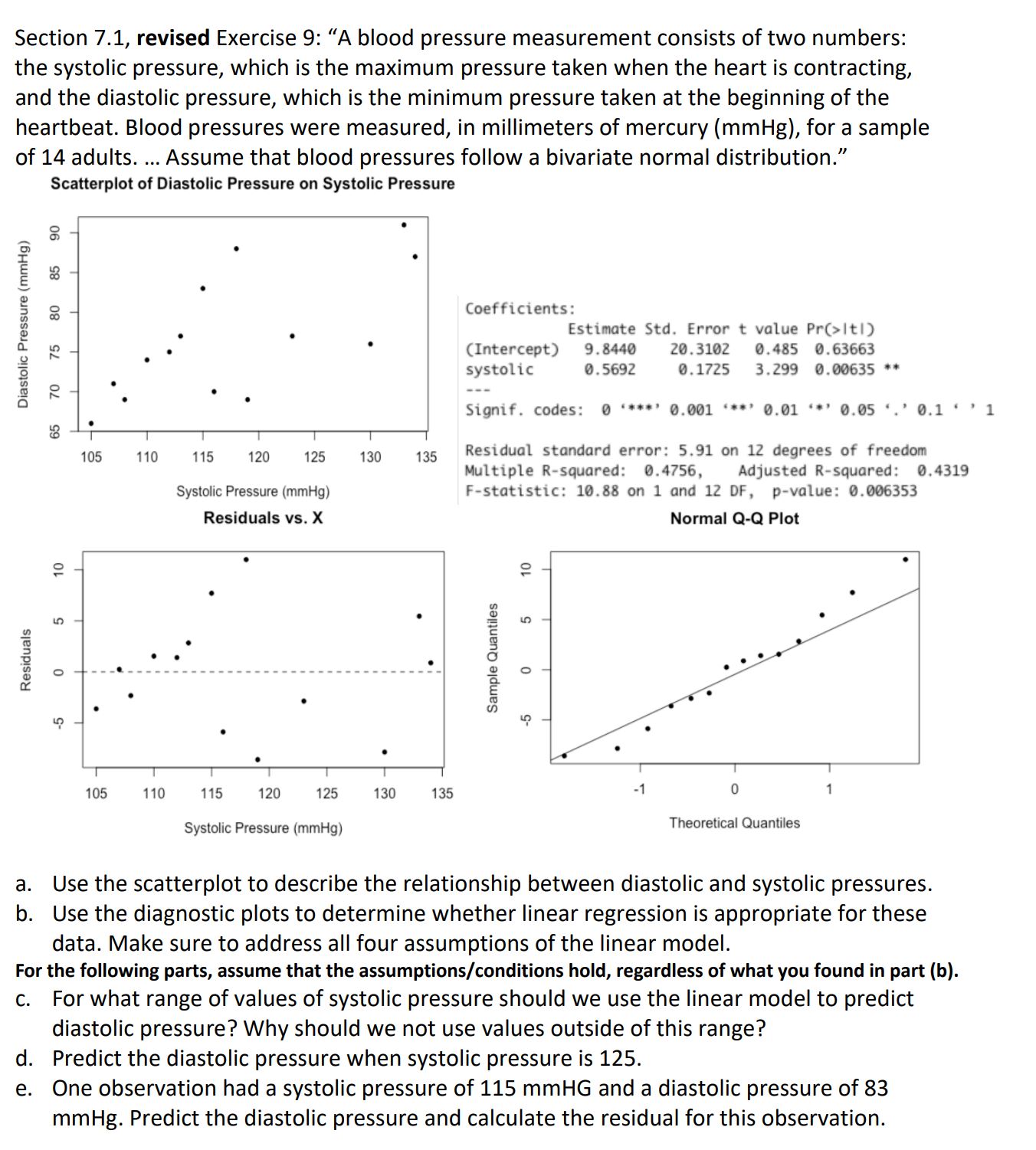
Section 7.1, revised Exercise 9: A blood pressure measurement consists of two numbers: the systolic pressure, which is the maximum pressure taken when the heart
Answered step by step
Verified Expert Solution
Question
42 users unlocked this solution today!
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1

Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
100% Satisfaction Guaranteed-or Get a Refund!
Step: 2Unlock detailed examples and clear explanations to master concepts

Step: 3Unlock to practice, ask and learn with real-world examples

See step-by-step solutions with expert insights and AI powered tools for academic success
-
 Access 30 Million+ textbook solutions.
Access 30 Million+ textbook solutions.
-
 Ask unlimited questions from AI Tutors.
Ask unlimited questions from AI Tutors.
-
 Order free textbooks.
Order free textbooks.
-
 100% Satisfaction Guaranteed-or Get a Refund!
100% Satisfaction Guaranteed-or Get a Refund!
Claim Your Hoodie Now!

Study Smart with AI Flashcards
Access a vast library of flashcards, create your own, and experience a game-changing transformation in how you learn and retain knowledge
Explore Flashcards





