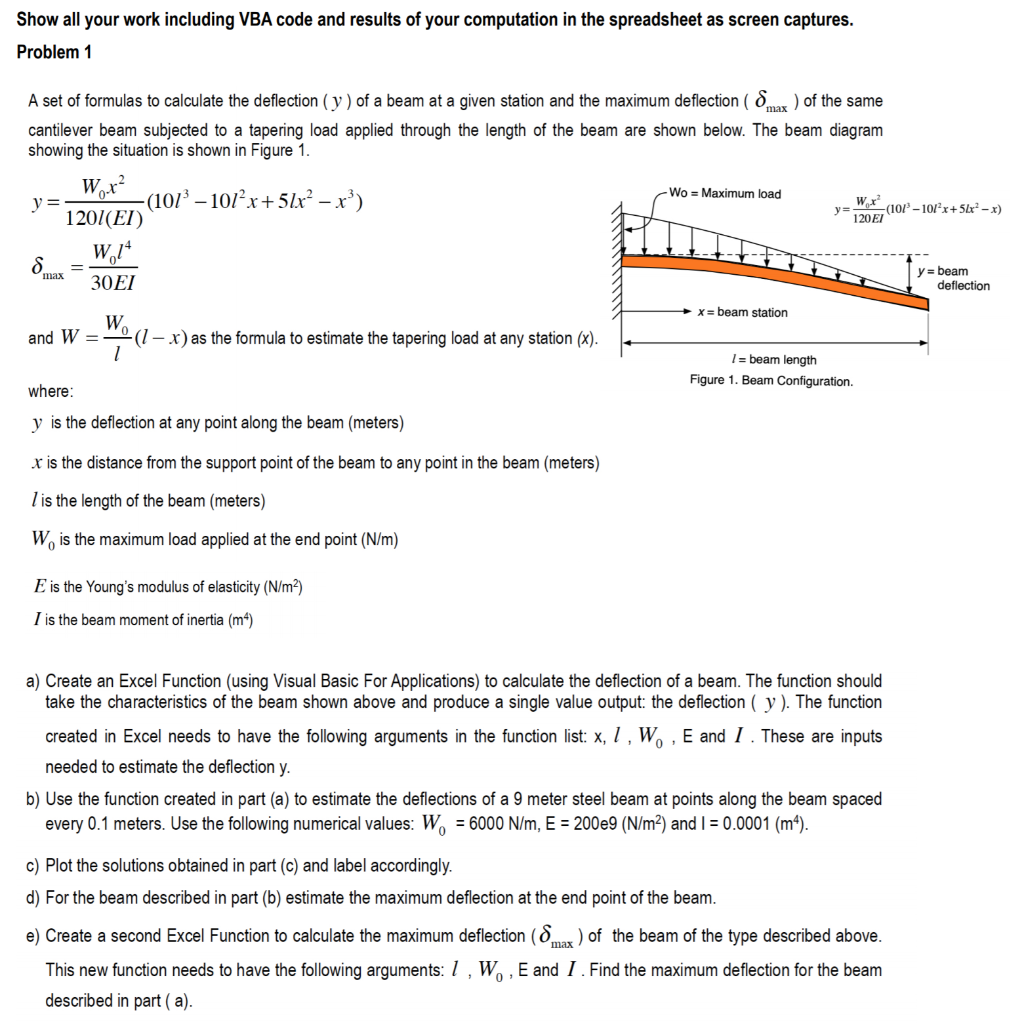
Show all your work including VBA code and results of your computation in the spreadsheet as screen captures. Problem 1 Wr y = 1201(EI) A set of formulas to calculate the deflection (y) of a beam at a given station and the maximum deflection (max) of the same cantilever beam subjected to a tapering load applied through the length of the beam are shown below. The beam diagram showing the situation is shown in Figure 1. Wox? -(101 - 1012x+51x x3) Wo = Maximum load (101 - 10/2x+52x2 - x) 120 EW W.14 30EI deflection x = beam station and W = 0 (1 - x) as the formula to estimate the tapering load at any station (X). 1 = beam length Figure 1. Beam Configuration. where: y is the deflection at any point along the beam (meters) y = beam x is the distance from the support point of the beam to any point in the beam (meters) l is the length of the beam (meters) W is the maximum load applied at the end point (N/m) E is the Young's modulus of elasticity (N/m2) I is the beam moment of inertia (m) a) Create an Excel Function (using Visual Basic For Applications) to calculate the deflection of a beam. The function should take the characteristics of the beam shown above and produce a single value output: the deflection (y). The function created in Excel needs to have the following arguments in the function list: x, 1 ,W , E and I. These are inputs needed to estimate the deflection y. b) Use the function created in part (a) to estimate the deflections of a 9 meter steel beam at points along the beam spaced every 0.1 meters. Use the following numerical values: W = 6000 N/m, E = 2009 (N/m2) and I = 0.0001 (m). c) Plot the solutions obtained in part (c) and label accordingly. d) For the beam described in part (b) estimate the maximum deflection at the end point of the beam. e) Create a second Excel Function to calculate the maximum deflection (max) of the beam of the type described above. This new function needs to have the following arguments: 1 ,W , E and 1. Find the maximum deflection for the beam described in part ( a). Show all your work including VBA code and results of your computation in the spreadsheet as screen captures. Problem 1 Wr y = 1201(EI) A set of formulas to calculate the deflection (y) of a beam at a given station and the maximum deflection (max) of the same cantilever beam subjected to a tapering load applied through the length of the beam are shown below. The beam diagram showing the situation is shown in Figure 1. Wox? -(101 - 1012x+51x x3) Wo = Maximum load (101 - 10/2x+52x2 - x) 120 EW W.14 30EI deflection x = beam station and W = 0 (1 - x) as the formula to estimate the tapering load at any station (X). 1 = beam length Figure 1. Beam Configuration. where: y is the deflection at any point along the beam (meters) y = beam x is the distance from the support point of the beam to any point in the beam (meters) l is the length of the beam (meters) W is the maximum load applied at the end point (N/m) E is the Young's modulus of elasticity (N/m2) I is the beam moment of inertia (m) a) Create an Excel Function (using Visual Basic For Applications) to calculate the deflection of a beam. The function should take the characteristics of the beam shown above and produce a single value output: the deflection (y). The function created in Excel needs to have the following arguments in the function list: x, 1 ,W , E and I. These are inputs needed to estimate the deflection y. b) Use the function created in part (a) to estimate the deflections of a 9 meter steel beam at points along the beam spaced every 0.1 meters. Use the following numerical values: W = 6000 N/m, E = 2009 (N/m2) and I = 0.0001 (m). c) Plot the solutions obtained in part (c) and label accordingly. d) For the beam described in part (b) estimate the maximum deflection at the end point of the beam. e) Create a second Excel Function to calculate the maximum deflection (max) of the beam of the type described above. This new function needs to have the following arguments: 1 ,W , E and 1. Find the maximum deflection for the beam described in part ( a)







