show how to use in excel with solver and answer the questions after please

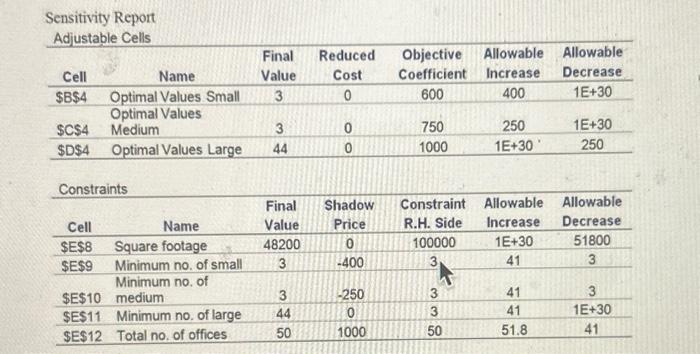

A real estate developer is planning to build an office complex. Currently, there are three office sizes under consideration: small, medium, and large. Small offices can be rented for $600 per month, medium offices can be rented for $750 per month, and large offices can be rented for $1000 per month. Each small office requires 600 square feet, cach medium office requires 800 square feet, and each large office requires 1000 square feet. The current plot of land available to the developer is 100,000 square feet. The devyloper wants to ensure that the office complex has at least 3 units of each office size. Moreover troning restrictions limit the total number of offices to 50 . Formulation: Let X1= no, of small offices to build X2= no. of medium offices to build X3= no. of large offices to build Max: 600X1+7502+1000X3 Subject to: 6001+8002+10003100,000 (square footage) X13 (minimum number of small offices) X23 (minimum number of medium offices) X33 (minimum number of large offices) X1+X2+X350 (maximum number of total offices) X1,X2, and X30 Sensitivity Report Part A) (10 points) Use the Sensitivity Report to answer the following questions: a. How many small, medium, and large offices should the developer build? b. What is the total optimal monthly revenue? c. Which constraints are binding? Which constraints are non-binding? d. How much square footage would remain unused if the developer implements the optimal solution? Part B) (20 points) Use the Sensitivity Report to answer the following questions: a. What would be the impact on the optimal allocation of offices and the objective function value if small offices can be rented for $800 per month rather than $600 per month? b. What would be the impact on the optimal allocation of offices and the objective function value if medium offices can be rented for $650 per month rather than $750 per month? c. What would be the impact on the optimal allocation of offices if medium offices can be rented for $1100.00 rather than $750 per month? d. Is the solution to the problem unique or are there alternate optimal solutions? Part C) (20 points) Use the Sensitivity Report to answer the following questions: a. Suppose that the square footage available to the developer increases to 110,000 square feet. What impact would this have on the optimal objective function value? b. Suppose that the minimal number of small officers that the developer needs to build must be at least 5 offices. What impact would this have on the optimal objective function value? c. Suppose that the monthly rental of small offices increases to $650, and that the monthly rental of medium offices increases to $800. What impact will this have on the current optimal solution and the objective function value? d. Suppose that the total number of officer) increases to a maximum of 55 , and the minimum number of medium offices increases to 5 . What impact would this have on the current optimal objective function value









