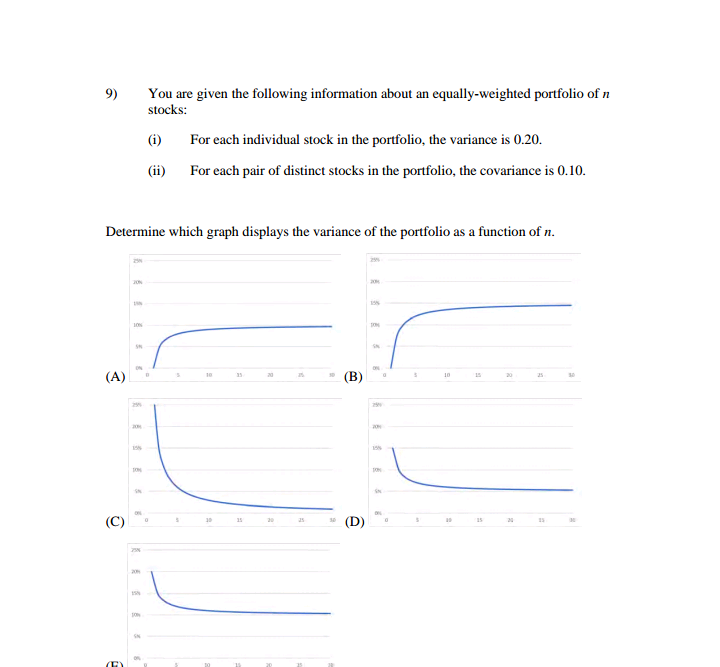
Show how you arrived at answer s

Expected Value of Sample Information Question 6. Ryoei Saito has received from the Siegfried Kramarsky family a take-it-or-leave-it offer to sell to Ryoei Saito the painting Portrait of Dr. Gachet, by Vincent van Gogh for $150 million. Ryoei Saito is an expected-value maximizer. Ryoei Saito has determined probability estimates of the painting's worth to other buyers, based on economic outcomes, as: P($120 million) = .3, P($140 million) = .4, P($160 million) = .1, and P($180 million) = .2 a. Should Ryoei Saito buy the painting? Explain your answer. b. What is the expected value of perfect information? Ryoei Saito can have an economic forecast performed by Christie's auction house. The forecast indicates either G = Good resale conditions or B = Bad resale conditions. Conditional probabilities of the indicators conditional on the collection's worth are P(G | $120 million) = .1, P(G | $140 million) = .3, P(G | $160 million) = .2, and P(G | $180 million) = .4 C. Should Ryoei Saito purchase that forecast if the forecast cost $1 million? What is the maximum amount Ryoei Saito should be willing to pay for that forecast?1. You are given that the ABC Stock price is traded at $45 now and the 3-month forward price is $46.80. Which of the following is true about outright purchase of this stock and the forward contract? (A) If the spot price is $45 after 3 months, the profit for outright purchase and long forward contract is the same (B) If the spot price is $46.80 after 3 months, the profit for outright purchase and long forward contract is the same. (C) If the ABC Stock pays a dividend of $0.50 after 1 month and is traded at $46.80 after 3 months, purchasing the stock outright makes a profit of $2.30. (D) If the ABC stock pays a dividend of $0.50 after 1 month and is traded at $46.80 after 3 months, the profit of long forward is $0. (E) The answer is not given in (A), (B), (C), and (D). 2. The current price of the Lucky Company Stock is $50, and the 6-month forward price is $52. What is the amount of money that needs to be lent today to mimic the profit of outright purchase after 6 months? Assume that the annual continuously compounded risk free rate is 5%. (A) $50.00 (B) $50.20 (C) $50.70 (D) $51.20 (E) $52.00 mple Questions 3. A dealer has just entered into a short forward position. The underlying asset is currently traded at $100 and the 1-year forward price is $105. Assuming an annual effective rate of 3%, find the number of 100 zero-coupon bonds that the dealer has to buy to hedge his position. (A) 0.00000 (B) 0. 19417 (C) 0.98058 (D) 1.019417 (E) 2.00000 4. Which of the following is false? (A) Entering into a long forward contract with a purchased zero-coupon bond maturing at the expiration date of forward mimics the payoff of an outright purchase of stock B) Purchasing a stock and borrowing the present value of forward price replicate a long forward contract (C) Entering into a long forward contract, selling a stock and buying a bond are always making a negative profit, since there is transaction cost. (D) Selling a stock and lending money at certain risk free rate earns the same payoff as a short forward contract (E) Forward contracts are the only derivative that has no credit risk involved1. A dealer has just entered into a derivative contract with a customer. The customer is obligated to sell the underlying asset to the dealer at the expiration date at price K. The dealer wishes to fully hedge his position by trading the following derivatives. Which of the followings achieves his goal? (A) Purchase a put option with strike price K (B) Sell a call option with strike price K (C) Purchase a K-strike call and sell a K-strike put D) Sell a K-strike call and purchase a K-strike put (E) Enter into a long forward contract with forward price at K 2. A dealer has just entered into a derivative position with a customer. The customer is obligated to sell the underlying asset to the dealer if the spot price at expiration is more than K, whereas the dealer has the right to sell the underlying asset to the customer if the spot price at expiration is less than K. Which of the followings describes the derivative trading? (A) The dealer purchases a K-strike call and a K-strike put B) The dealer sells a K-strike call and purchases a K-strike put (C) The dealer purchases a K-strike call and sells a K-strike put (D) The dealer sells a K-strike call and a K-strike put (E) The dealer enters into a long forward contract Guestions 3. Alan has just entered into a derivative position with a dealer. The dealer makes a positive payoff when the price of underlying asset is less than $35 and higher than $45 at expiration. Which of the followings describes the option strategy that the dealer has entered into? 1. 35-45 purchased strangle II. 35-45 written strangle Ill. 35-40-45 butterfly-spread IV. 35-45 Bull call spread (A) I, III (B) II, III (C) II, IV (D) III, IV (E) No answer is given in (A), (B), (C), and (D)3) You are given the following information about the annual returns of two stocks, X and Y: The expected returns of X and Y are E[ Rx] = 10% and E[Ry] = 15%. ii) The volatilities of the returns are V =18% and V =20% . 111) The correlation coefficient of the returns for these two stocks is 0.25. iv) The expected return for a certain portfolio, consisting only of stocks X and Y, is 12%. Calculate the volatility of the portfolio return.9) You are given the following information about an equally-weighted portfolio of n stocks: (i) For each individual stock in the portfolio, the variance is 0.20. (ii) For each pair of distinct stocks in the portfolio, the covariance is 0.10. Determine which graph displays the variance of the portfolio as a function of n. (A) 10 20 (B) 10 25 (C) 15 25 (D) 1510) You are given the following information about three stocks (X, Y, and Z) in a portfolio: (i) The covariance matrix for each stock with each other stock is given in the following table: X Z X 0.040 -0.018 0.016 Y -0.018 0.090 -0.021 Z 0.016 -0.021 0.010 (ii) The weighting of each stock in the portfolio is as follows: Stock | Weighting X 30% 20% 50% Calculate the variance of this portfolio. (A) 0.0081 (B) 0.0089 (C) 0.0123 (D) 0.0902 (E) 0.0944