Show step by$-$step procedures on how to reach the final answer. If a formula is used, write down the formula before plugging in numbers; also provide a brief justification for the choice of the formula

Problem A$3$: Valuation of stock options & Greeks

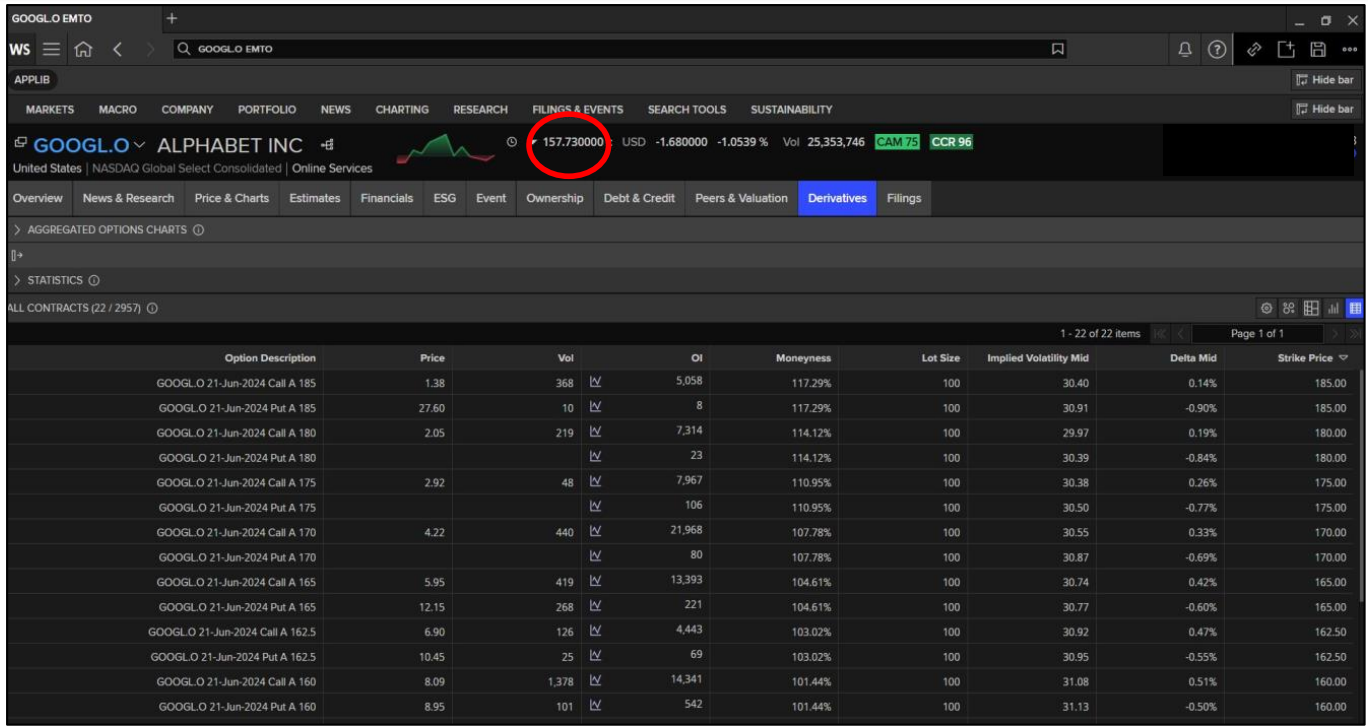
In this question, you need to price options with different option valuation approaches. The figure

below, extracted from Refinitiv Workspace, shows information for stock options on Alphabet$$s

$($Google$)$ stock. Assume today is $21$ April $2024.$ Consider the options with the strike price of $$165.$

The option maturity is $21$ June $2024.$ Assume the benchmark risk$-$free interest rate is $5\%$ per

annum with continuous compounding for all maturities. Assume that the share price today is

$$157\mathrm{.}73$ and has a volatility of $30\%$ per annum.

Note: Ignore day count conventions and assume that one month $=1/12$ of the year, two months $=2/12$ of the year.

Figure $1.$ Screen shot of Alphabet options $($Refinitiv Workspace$)$ a$.$ Calculate the up movement size in one month u and the down movement size d and round

these to the nearest second decimal place $[$i$.$e$.$ if u$=1\mathrm{.}05733,$ use $1\mathrm{.}06].$

b$.$ Calculate the probability p of the stock price moving up in one month in the risk$-$neutral world.

c$.$ Draw a binomial tree to show the stock price movement in the next two one$-$month periods.

d$.$ Use a two$-$step binomial tree to calculate the value of a two$-$month European call option

based on the no$-$arbitrage approach.

e$.$ Use a two$-$step binomial tree to calculate the value of a two$-$month European call option

based on the risk$-$neutral valuation.

f$.$ Use a two$-$step binomial tree to calculate the value of a two$-$month European put option

based on the risk$-$neutral valuation.

g$.$ Use a two$-$step binomial tree to calculate the value of a two$-$month American put option.

h$.$ Without calculations, show the American call option price if we assume the company will not

pay dividends during the option life and explain your approach

i$.$ Show whether the put$-$call$-$parity holds for the European call and the European put prices

you just calculated in $[$e$]$ and $[$f$].$

j$.$ Compare the put option prices you have just calculated with the actual put option price $($using

the Price column$)$ shown in the figure. Why are there differences? Briefly discuss some

possible reasons.

k$.$ What is the Black$-$Scholes$-$Merton price of a two$-$month European call option?

l$.$ What is the Black$-$Scholes$-$Merton price of a two$-$month European put option?

m$.$ Without calculations: What would happen to the option prices you just calculated in $[$k$]$ and

$[$l$]$ if the interest rate increases to $6\%?$ Why?

n$.$ Calculate the Black$-$Scholes deltas of the put and the call.

o$.$ Compare the call option prices you just calculated in $[$e$]$ and $[$k$].$ Compare also the put option

prices you calculated in $[$f$]$ and $[$l$].$ Do you expect these prices to be the same? Why$/$Why

not?

p$.$ Finally, assume that you have a position in $2,000$ options. Using your results from $[$n$],$ show

how you can delta$-$hedge your position if

$$ your position is a short position in $2,000$ European calls.

$$ your position is a short position in $2,000$ European puts.

$$ your position is a short position in $1,500$ European calls and $500$ European puts.