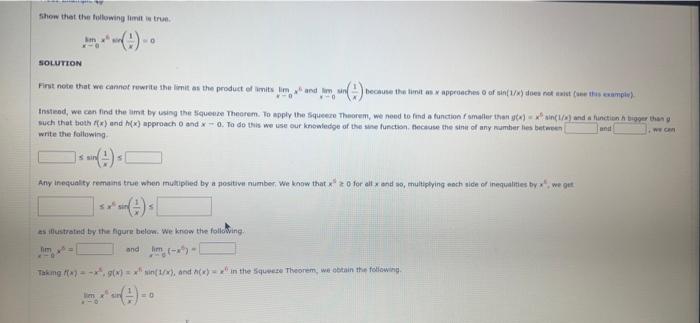
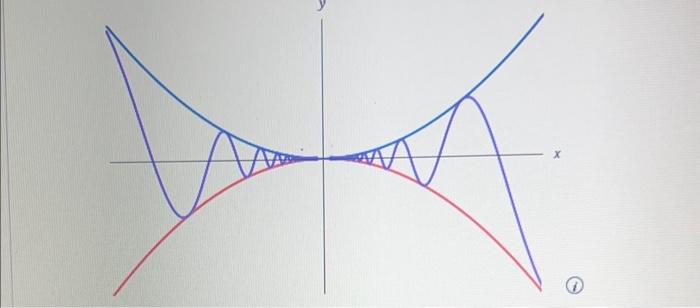
Show that the following limit is true. SOLUTION -O First note that we cannot rewrite the limit as the product of limits lim, and lim sin 0 because the limit as x approaches 0 of sin(1/x) does not exist (see this example). Instead, we can find the limit by using the Squeeze Theorem. To apply the Squeeze Theorem, we need to find a function f smaller than g(x)=x sin(1/x) and a function A bigger than y such that both f(x) and h(x) approach 0 and x-0. To do this we use our knowledge of the sine function. Because the sine of any number les between write the following. and We can sin Any inequality remains true when multiplied by a positive number. We know that x 20 for all x and so, multiplying each side of inequalities by x, we get sx sin as illustrated by the figure below. We know the following. m: and lim (-x)- Taking f(x), g(x) = x sin(1/x), and h(x) in the Squeeze Theorem, we obtain the following. sin =O