show the easiest steps

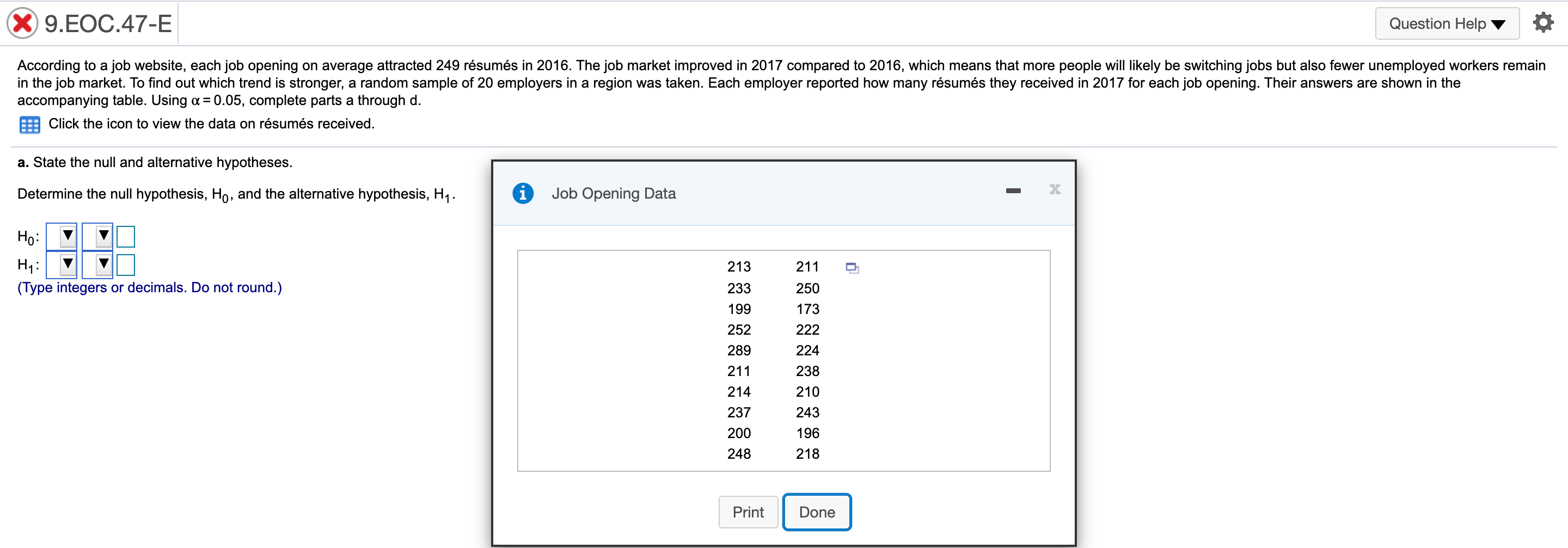
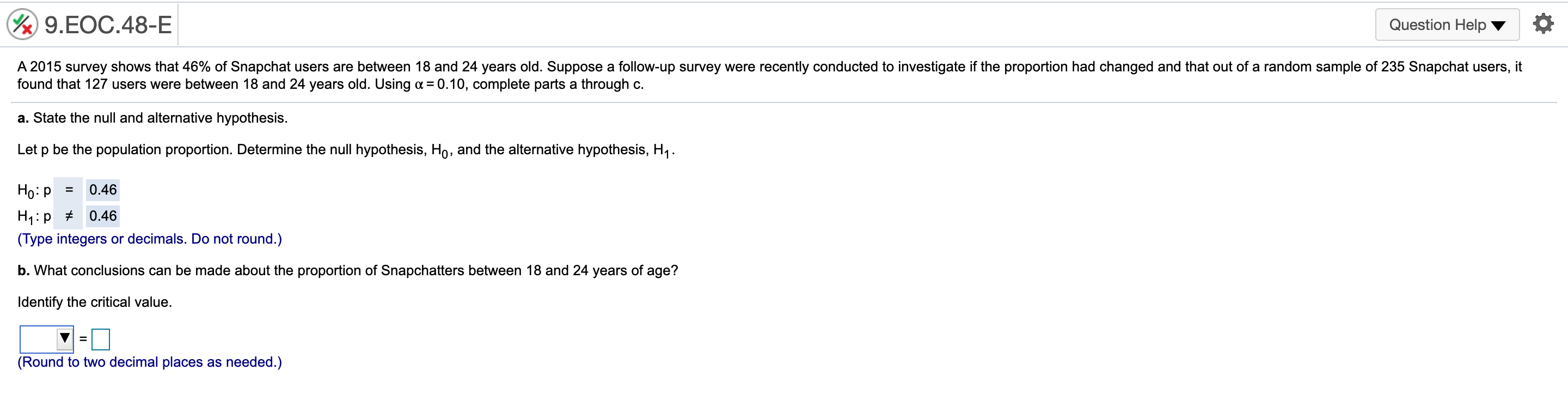
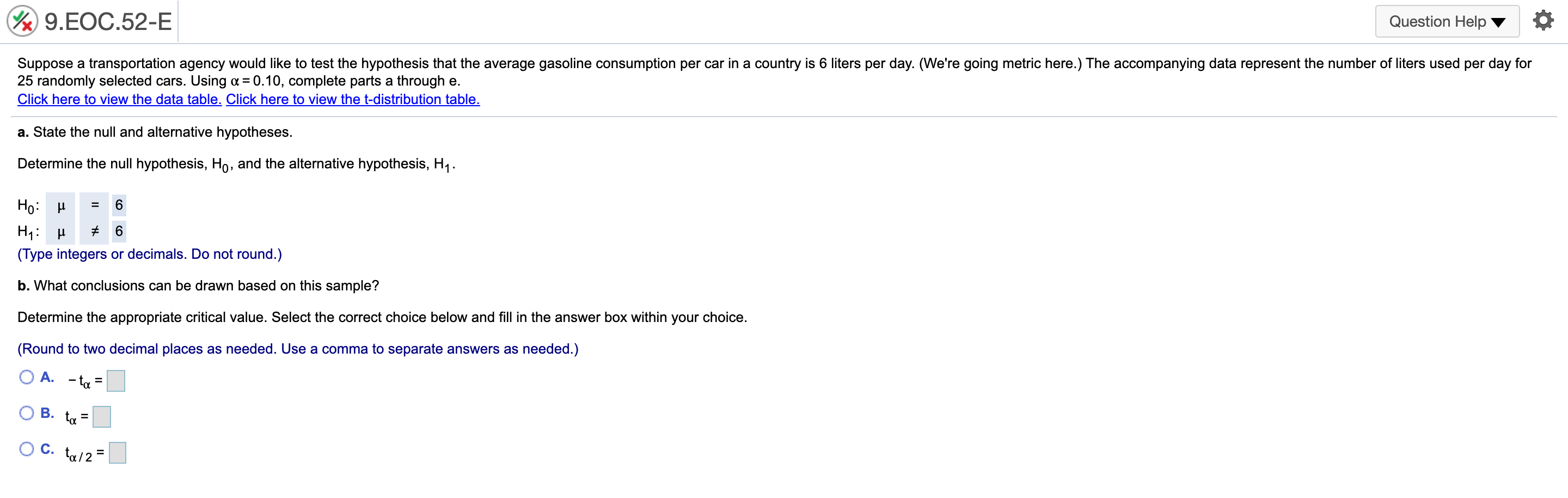
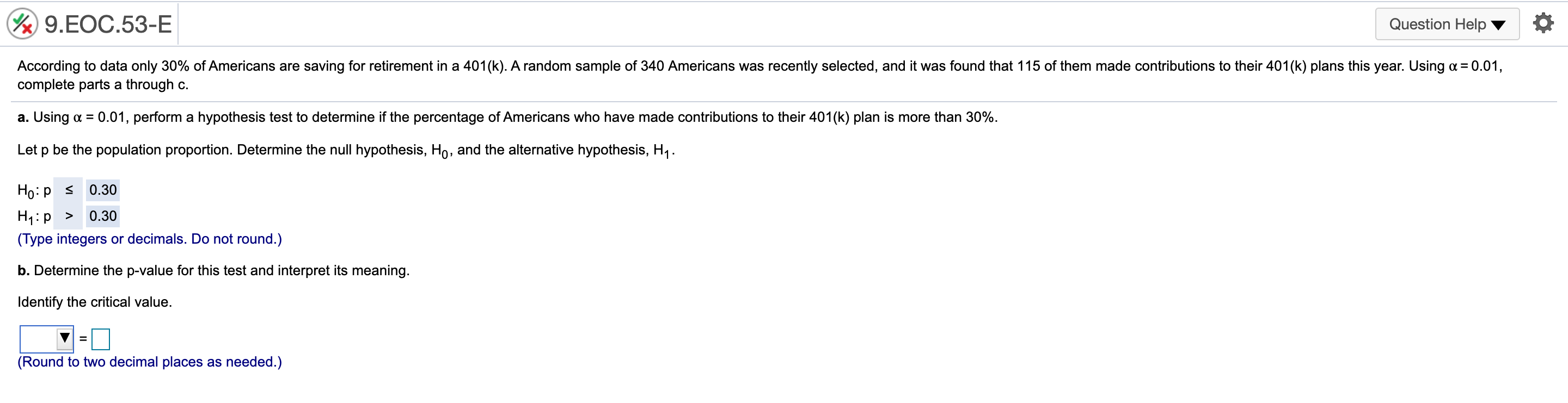
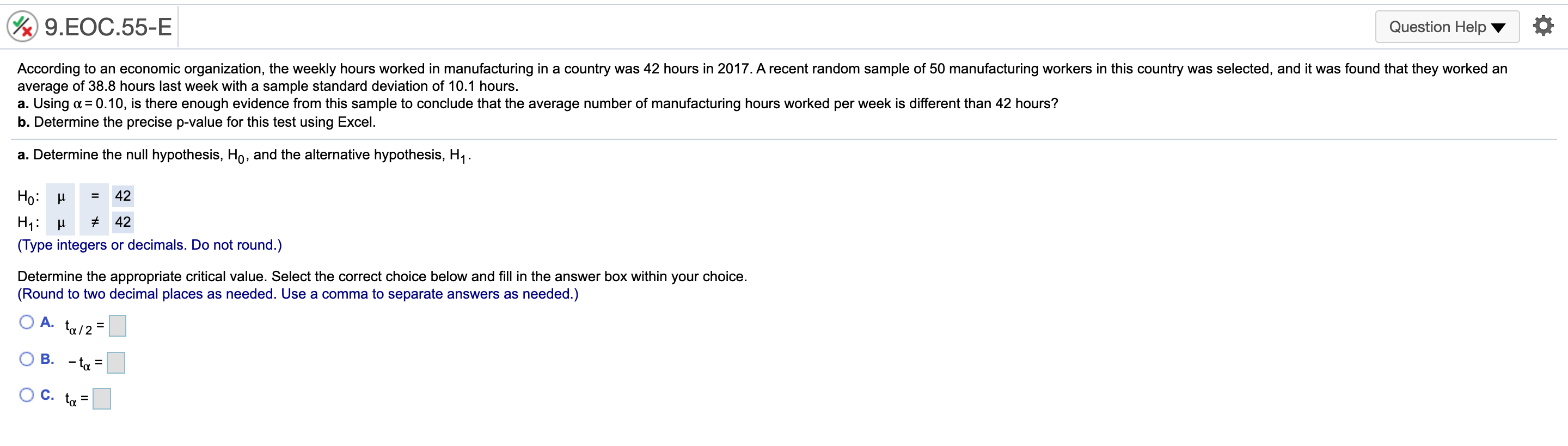
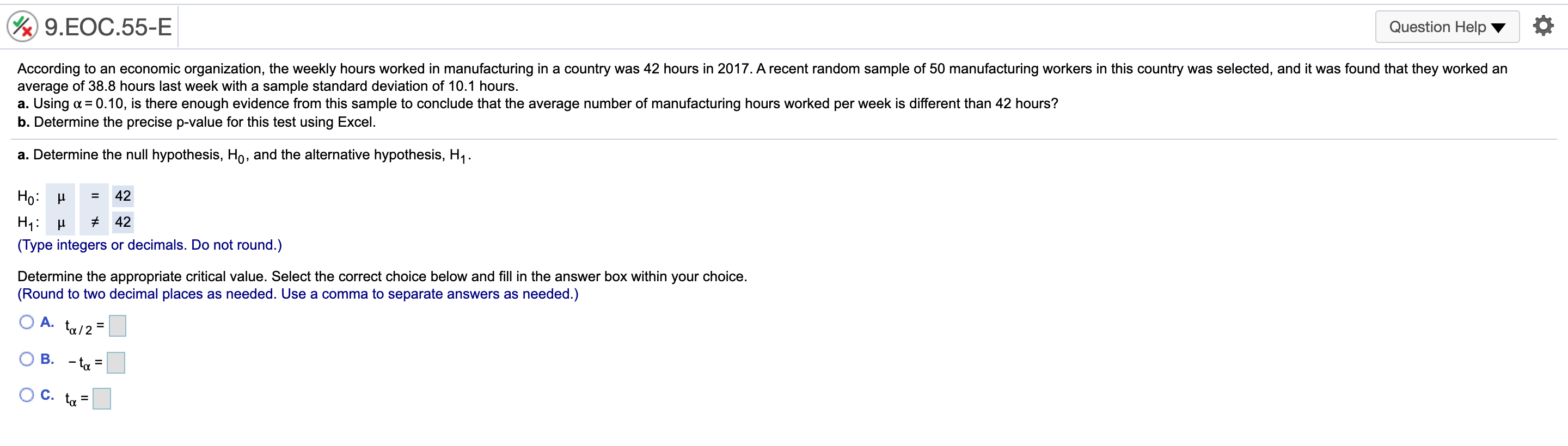
9.EOC.44-E Question Helpv , 0 According to a 2016 report, 40% of 18-to-20-yearold students use credit cards for everyday purchases. Suppose a local bank believes that this share will increase over time because of shopping behaviors of students To test this hypothesis, a random sample of 279 students was selected, 131 of whom use credit cards for everyday purchases. Using a = 0.05, complete parts a through ct a. State the null and alternative hypothesis, Let p be the population proportion. Determine the null hypothesis, H0, and the alternative hypothesis, H1 . Ho:p V H1:p V (Type integers or decimals. Do not round) 9.EOC.45-E Question Helpv at A poll from 2016 showed that the share of Americans who are "extremely proud\" to be American has been steadily decreasing since 2000 to 53% in 2016. Suppose the White House staff is concemed that the rating has fallen further. Let's say that out of a random sample of 400 adults, 192 stated that they were "extremely proud\" to be American. Using or = 0.05, complete parts a through d. a. State the null and alternative hypothesis Let p be the population proportion. Determine the null hypothesis, Ho, and the alternative hypothesis, H1. H0: p 2 0.53 H1: p 0.30 (Type integers or decimals. Do not round.) h. Determine the p-value for this test and interpret its meaning. Identify the critical value. I: (Round to two decimal places as needed.) 9EOC55-E Question Helpv ' 0 According to an economic organization. the weekly hours worked in manufacturing in a country was 42 hours in 2017. A recent random sample of 50 manufacturing workers in this country was selected. and it was found that they worked an average of 3&8 hours last week with a sample standard deviation of 10.1 hours. a. Using a: 0.10, is there enough evidence from this sample to conclude that the average number of manufacturing hours worked per week is different than 42 hours? b. Determine the precise p-value for this test using Exoel. 3. Determine the null hypothesis, Ho, and the alternative hypothesis, H1. Ho: 1; = 42 H1: [1 at 42 (Type integers or decimals. Do not round) Determine the appropriate critical value. Select the correct choice below and ll in the answer box within your choice. (Round to two decimal places as needed, Use a comma to separate answers as needed.) 0 A' 1m/z = O B. -1\": O C. rd: @ 9..EOC58-E Question Helpv '6 During 2016, the average monthly bill for digital cable in a country was $105. Suppose a cable company would like to test the hypothesis that the average monthly bill is higher than $105 this year. A random sample of 48 households was chosen, Assume the standard deviation of monthly cable bills in the country is $19. Complete parts a through d. Explain how a Type I error can occur. Choose the correct answer below. A. The average monthly cable bill is greater than $105, but based on the sample it is incorrectly concluded that the average monthly cable bill is less than or equal to $105. 3 B. The average monthly cable bill is less than or equal to $105, but based on the sample it is incorrectly concluded that the average monthly cable bill is greater than $105. C. The average monthly cable bill has changed from $105, but based on the sample it is incorrectly concluded that the average monthly cable bill has not changed from $105. D. The average monthly cable bill is equal to $105, but based on the sample it is incorrectly concluded that the average monthly cable bill has changed from $105. Explain how a Type II error can occur. Choose the correct answer below. A. The average monthly cable bill is equal to $105, but based on the sample it is incorrectly concluded that the average monthly cable bill has changed from $105. 3 B. The average monthly cable bill is greater than $105, but based on the sample it is incorrectly concluded that the average monthly cable bill is less than or equal to $105. C. The average monthly cable bill has changed from $105, but based on the sample it is incorrectly concluded that the average monthly cable bill has not changed from $105. D. The average monthly cable bill is less than or equal to $105, but based on the sample it is incorrectly concluded that the average monthly cable bill is greater than $105. b. Using a = 0,05, compute the probability of a Type II error occurring if the actual average monthly cable bill is $113. The probability is 0.102 . (Round to three decimal places as needed.) c. Using a: 0.10, compute the probability of a Type II error occurring if the actual average monthly cable bill is $113. The probability is . (Round to three decimal places as needed.) @ 9..EOC59-E Question Helpv O The average wait time on the phone for taxpayers calling a tax agency in 2015 was 1,342 seconds. Suppose the tax agency made operational changes in an altar! to reduce wait limes. To test the effectiveness of these changes. a random sample of 51 phone calls was selected and the wait time of each call was recorded. Assume the standard deviation for the wait time is 250 seconds. Complete parts a through d. Explain how a Type I error can occur. Choose the correct answer below. A. The average wait time has changed from 1,342 seconds, but based on the sample it is incorrectly concluded that the average wait time has not changed from 1,342 seconds. 3 B. The average wait time is greater than or equal to 1,342 seconds, but based on the sample it is incorrectly concluded that the average wait time is less than 1,342 seconds. 0. The average wait time is equal to 1,342 seconds, but based on the sample it is incorrectly concluded that the average wait time has changed from 1,342 seconds. D. The average wait time is less than 1,342 seconds, but based on the sample it is incorrectly concluded that the average wait time is greater than or equal to 1.342 seconds. Explain how a Type II error can occur. Choose the correct answer below. A. The average wait time is equal to 1,342 seconds, but based on the sample it is incorrectly concluded that the average wait time has changed from 1,342 seconds. 3 B. The average wait time is less than 1,342 seconds, but based on the sample it is incorrectly concluded that the average wait time is greater than or equal to 1,342 seconds. C. The average wait time has changed from 1.342 seconds, but based on the sample it is incorrectly concluded that the average wait time has not changed from 1.342 seconds. D. The average wait time is greater than or equal to 1.342 seconds. but based on the sample it is incorrectly concluded that the average wait time is less than 1.342 seconds. b. Using or = 0.01, compute the probability of a Type II error occurring if the actual average wait time per call is 1.258 seconds. The probability is 0.471 . (Round to three decimal places as needed.) c. Using a: 0.01, compute the probability of a Type II error occurring if the actual average wait time per call is 1,189 seconds. The probability is . (Round to three decimal places as needed.) @ 9HE0061-E Question Helpv 0 According to a country's department of labor, 11.4% of the country's workforoe was unionized in 2017. Suppose the department would like to test the hypothesis that the proportion of union workers decreased in 2018 by randomly sampling 177 employees. Complete parts a through d. Explain how a Type I error can occur. Choose the correct answer below. A. The percentage of unionized employees is less than 11.4%, but based on the sample it is incorrectly concluded that the percentage of unionized employees is not less than 11.4%. B. The percentage of unionized employees has changed from 11.4%, but based on the sample it is incorrectly concluded that the percentage of unionized employees has not changed from 11.4%. C. The percentage of unionized employees is equal to 11.4%, but based on the sample it is incorrectly concluded that the percentage of unionized employees has changed from 11.4%. s\" D. The percentage of unionized employees is greater than or equal to 11.4%, but based on the sample it is incorrectly concluded that the percentage of unionized employees is less than 11.4%. Explain how a Type II error can occur. Choose the correct answer below. A. The percentage of unionized employees has changed from 11.4%, but based on the sample it is incorrectly concluded that the percentage of unionized employees has not changed from 11.4%. B. The percentage of unionized employees is greater than or equal to 11.4%, but based on the sample it is incorrectly concluded that the percentage of unionized employees is less than 11.4%. .V C. The percentage of unionized employees is less than 11.4%, but based on the sample it is incorrectly concluded that the percentage of unionized employees is not less than 11.4%. D. The percentage of unionized employees is equal to 11.4%, but based on the sample it is incorrectly concluded that the percentage of unionized employees has changed from 11.4%. b. Using a = 0.05, compute the probability of a Type II error occurring if the actual proportion of unionized employees in the workforce is 8%. The probability is 0.603 . (Round to three decimal places as needed.) c. Using a: 0.05, compute the probability of a Type II error occurring if the actual proportion of unionized employees in the workforce is 4%. The probability is . (Round to three decimal places as needed.)