show the fotmulas that you use in the excel, please!

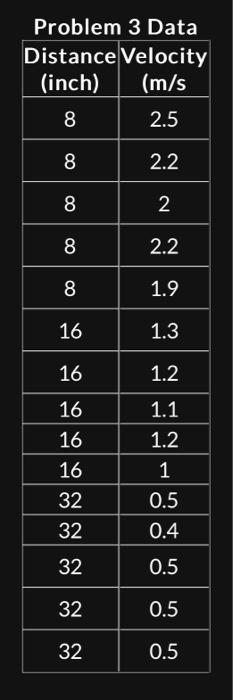
Instructions 1. Open a new Excel Workbook. 2. Solve each of the problems shown below in a separate Worksheet. 3. Rename each worksheet (Tab) per problem number. 4. Save your workbook (containing all the worksheets) using your name and assignment number as the file name. Example: JohnDoe1.xlsx 5. Upload your Excel file and submit the assignment. Solution Requirements 1. Apply problem solving methodology to solve each of the problems shown below. 2. Use absolute cell reference where appropriate. 3. Use Cell and Number formatting for better presentation. 4. Include headings, titles and labels on all Tables and Graphs. Assignment Problems 1. Create a surface plot of F(x,y)=sin({(x/4)2+(y/9)2}) for 8x8 and 8y8. Use 0.5 as increment, i.e. x=8,7.5,7..7,7.5,8 2. Create an Excel table containing the data shown below: (a) Sort the data from smallest to largest. (b) Plot the sorted discrete data (use X-Y Scatter chart type). (c) Draw a 3rd order polynomial trendline though the data, and show the trendline equation on the graph. (d) Using the trendline equation estimate how many cars someone who has been working for 8 weeks can be expected to inspect? (Note they can only inspect whole cars, no fractions. So use ROUNDO function for final answer.) 3. Create an Excel table containing the data shown below (use copy and paste to Excel) (a) Convert the distance from inch to meter (use CONVERTO function) (b) Plot the discrete data set Air Velocity (m/s) vs. Distance (m) (note distance is in meters and is plotted on the horizontal axis of a X Y Scatter chart). (c) Draw an exponential trendline through the data set, and show the trendline equation on the graph. (d) Using the trendline equation find the Air Velocity estimate for a distanke of 9 inches (remember the equation is based on data plotted which is in SI units so convert distance to ' m ' before substituting into the equation). Problem 3 Data Distance Velocity \begin{tabular}{|c|c|} \hline (inch) & (m/s \\ \hline 8 & 2.5 \\ \hline 8 & 2.2 \\ \hline 8 & 2 \\ \hline 8 & 2.2 \\ \hline 8 & 1.9 \\ \hline 16 & 1.3 \\ \hline 16 & 1.2 \\ \hline 16 & 1.1 \\ \hline 16 & 1.2 \\ \hline 16 & 1 \\ \hline 32 & 0.5 \\ \hline 32 & 0.4 \\ \hline 32 & 0.5 \\ \hline 32 & 0.5 \\ \hline 32 & 0.5 \\ \hline \end{tabular}