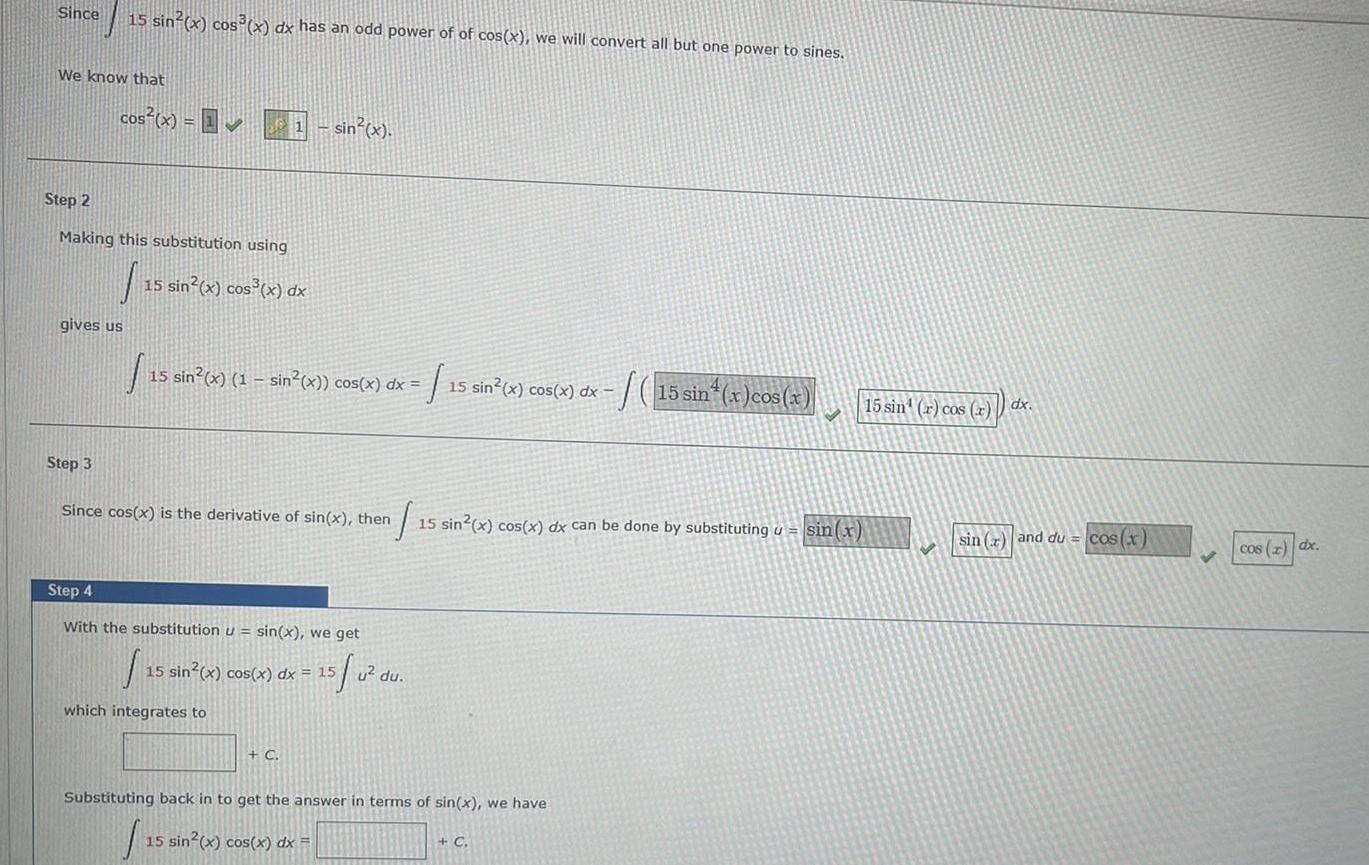
Since 15 sin(x) cos(x) dx has an odd power of of cos(x), we will convert all but one power to sines. We know that COS(x) = 1 - sin(x). Step 2 Making this substitution using gives us | 15 15 sin(x) cos(x) dx 15 sin(x) (1-sin(x)) cos(x) dx = 15 sin(x) cos(x) dx 15 sin(x)cos(x) 15 sin (r) cos (r)dx. Step 3 Since cos(x) is the derivative of sin(x), then 15 sin(x) cos(x) dx can be done by substituting u=sin(x) sin(x) and du= cos(x) cos (z) dx. Step 4 With the substitution u = sin(x), we get 15 sin(x) cos(x) dx = 15 = 15/u 2 du. which integrates to + C. Substituting back in to get the answer in terms of sin(x), we have 15 sin(x) cos(x) dx = + C.