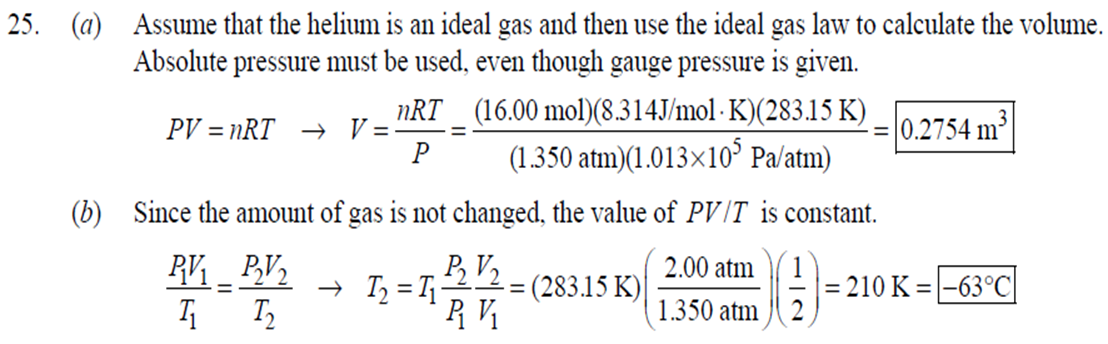
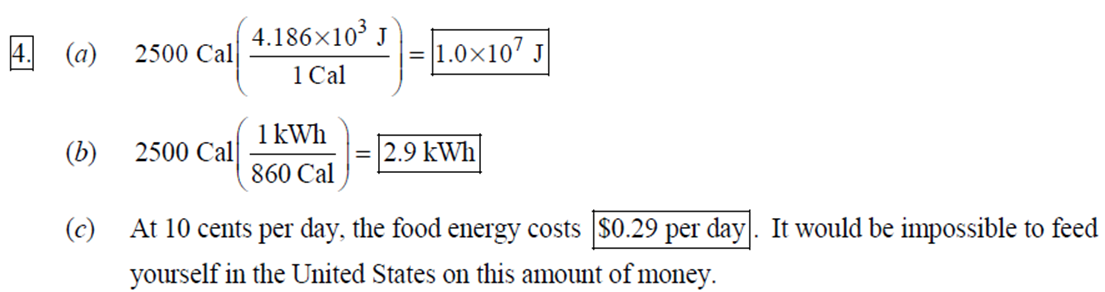
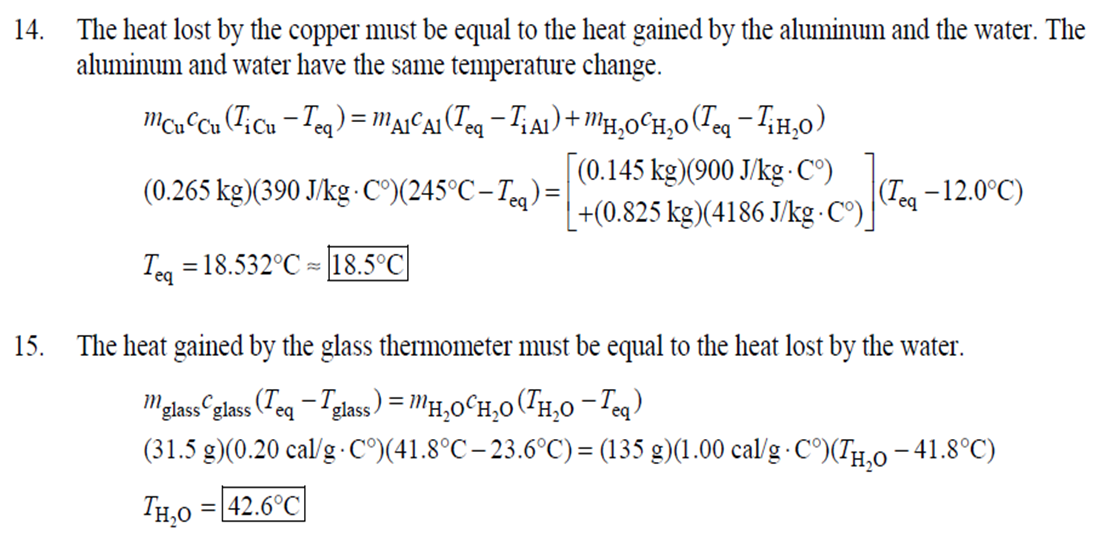
1. 2. The number of atoms in a pure substance can be found by dividing the mass of the substance by the mass of a single atom. Take the atomic masses of gold and silver from the periodic table. 2.75102 kg NAu (196.96655 u/atom)(1.6610-27 kg/u) 107.8682 NAS 2.75102 kg -2 (107.8682 u/atom)(1.661027 kg/u) = 0.548 NAu = 0.548N Ag 196.96655 Because a gold atom is heavier than a silver atom, there are fewer gold atoms in the given mass. The number of atoms is found by dividing the mass of the substance by the mass of a single atom. Take the atomic mass of copper from the periodic table. NCu 3. (a) 3.4103 kg (63.546 u/atom)(1.661027 kg/u) T(C)=[T(F)-32]=[68-32] = 20C 3.21022 atoms of Cu (b) T(F) = (C)+32=-3(1900) + 32 = 3452F = [3500F] 4. High: T(C) = {[T(F) 32] = [13632]=[57.8C| Low: T(C)= [T(F)-32]=[-129-32]=-89.4C 5. T(F)=(C)+32= {(38.9C) +32= 102.0F] 6. (a) T(F) = (C) +32=3(-18)+32 = 0.4F = [0F (b)T(C)=[T(F) 32]=[18-32]=27.78C = |28C| 22 7. The two temperatures, as given by the conversions, are to be the same. T(F) = T (C) +32 > x=2x+32 -32=x x=(-32)=-40 Thus, -40C = -40F 9. 10. 11. 12. Take the 300-m height to be the height in January. Then the increase in the height of the tower as the temperature rises is given by Eq. 13-1a. Al = lAT = (1210/C)(300 m)(25C -2C) = |0.08 m| When the concrete cools in the winter, it will contract, and there will be no danger of buckling. Thus, the low temperature in the winter is not a factor in the design of the highway. But when the concrete warms in the summer, it will expand. A crack must be left between the slabs equal to the increase in length of the concrete as it heats from 15C to 50C. Al = lAT = (12106/C)(12 m)(50C -15C) = 5.0103 m The increase in length of the table is given by Eq. 13-1a. Al=l AT = (0.20106/C)(1.8 m)(6.0 C) = 2.2106 m For steel, Al = alAT = (12106/C)(1.8 m)(8.0 C) = 1.710 m. The change for Super Invar is only 6 of the change for steel. The increase in length of the rod is given by Eq. 13-1a. 0.015 Al=AT = T = T +- =25C+ = 814.5C= 810C alo alo 1910-6/C 21. 22. 23. 24. Use the relationship that T(K) = {[T(F) 32]+273.15. T(K)= [T(F)-32]+273.15 T(F) = [T(K) 273.15]+32 = {}{[0 K 273.15]+32 = |459.67F| Use the relationship that T(K) =T(C) +273.15. (a) T(K) =T(C)+273.15 = 4270 K = 4300 K|; T(K) = T(C) +273.15 = 15106 K (b) 4000C: AT % error = T(K) 273.15 4270 -100= 273.15 T(K) -X100 1006.4% 15106 C: 273.15 15106 -X100 = 1.8103% Assume the gas is ideal. Since the amount of gas is constant, the value of PV/T is constant. = PV1 P2V2 T T V =V 1, P T = = (3.50 m) 1.00 atm (273+38.0) K 3.20 atm 273 K = 1.25 m Assume the air is an ideal gas. Since the amount of air is constant, the value of PV/T is constant. RV RV = 41 P2 V2 P V 40 atm 1 == (293 K) = 1302 K=1029C=1000C 1 atm 9 25. (a) Assume that the helium is an ideal gas and then use the ideal gas law to calculate the volume. Absolute pressure must be used, even though gauge pressure is given. PV = nRT V = nRT P (16.00 mol)(8.314J/molK)(283.15 K) (1.350 atm)(1.013105 Pa/atm) 0.2754 m (b) Since the amount of gas is not changed, the value of PV/T is constant. = T PV PV 12 1 = 1 - P2V2 RV 2.00 atm = (283.15 K) 210 K=-63C 1.350 atm 2 26. Assume that the nitrogen and carbon dioxide are ideal gases and that the volume and temperature are P RT is constant. Also note that n V constant for the two gases. From the ideal gas law, the value of = concerning the ideal gas law, the identity of the gas is unimportant, as long as the number of moles is considered. = P P m 12 21.6 kg CO2 44.01103 kg CO2/mol n n P = R = (3.45 atm) 2.20 atm 21.6 kg N 28.01103 kg N/mol 27. (a) Assume the nitrogen is an ideal gas. The number of moles of nitrogen is found from the atomic weight, and then the ideal gas law is used to calculate the volume of the gas. n=(28.5 kg)- 1 mole N 28.0110-3 kg = 1017 mol NRT PV = nRT V= = P (1017 mol)(8.314J/molK)(273 K) 22.79 m 1.013105 Pa = (b) Hold the volume and temperature constant and again use the ideal gas law. n = (28.5 kg+32.2 kg)- 1 mole N 28.01103 kg = 2167 mol PV = nRT -> P = nRT (2167 mol)(8.314J/mol K)(273 K) = 2.16105 Pa = 2.13 atm V 22.79 m 22.8 m 38. At STP, 1 mole of ideal gas occupies 22.4 L. 1 mole 6.021023 molecules 22.4 L mole 1L 2.691025 molecules/m m 39. We assume that the water is at 4C, so its density is 1000 kg/m. 3 10-3 m 1000 kg 1.000 L 1L 1m 1 mol (15.9994+21.00794)10 kg 55.51 mol 6.0221023 molecules 55.51 mol 3.3431025 molecules 1 mol 40. (a) Since the average depth of the oceans is very small compared to the radius of the Earth, the ocean's volume can be calculated as that of a spherical shell with surface area 47Rarth and a thickness Ay. Then use the density of sea water to find the mass and the molecular weight of water to find the number of moles. Volume = 0.75(47 REarth )Ay = 0.75(47)(6.38106 m) (310 m) = 1.15108 m 1.151018 m 1025 kg 1 mol 3 m 18103 kg = 6.551022 moles = 71022 moles (b) 6.551022 moles (6.021023 molecules/1 mol) = 41046 molecules 41. Assume the gas is ideal at those low pressures and use the ideal 42. N PV = NkT > V = P kT = gas law. 1x10-12 N/m (1.3810-23 J/K)(273 K) 3108 molecules 10-6 m m 1 cm = 300 molecules/cm is 22.4 L. We We assume an ideal gas at STP. Example 13-9 shows that the molar volume of this gas calculate the actual volume of one mole of gas particles, assuming a volume of (3), and then find the ratio of the actual volume of the particles to the volume of the gas. V molecules (6.021023 molecules)((3.010-10 m)/molecule) (22.4 L)(1103 m/1L) V gas The molecules take up less than 0.1% of the volume of the gas. 43. (a) = 7.3x104 The average translational kinetic energy of a gas molecule is 22KT. KE avg = kT = (1.3810-23 J/K)(273 K) = 5.6510-21 J (b) The total translational kinetic energy is the average kinetic energy per molecule times the number of molecules. KE total = N(KE avg) = (1.0 mol) 6.021023 molecules 1 mol (1.381023 J/K)(298 K) = 3700 J 1. The kilocalorie is the heat needed to raise 1 kg of water by 1 C. Use this relation to find the change in the temperature. (8200 J) 1 kcal (1 kg)(1C) { 1 4186J 1 kcal = = 0.653 C 3.0 kg Thus, the final temperature is 10.0C +0.653C = 10.7C| 2. The kilocalorie is the heat needed to raise 1 kg of water by 1 C. Use the definition to find the heat needed. (34.0 kg)(95C-15C)- 1 kcal (1 kg)(1 C) 4186 J 1 kcal |=1.139107 J=1.1107 J 3. Find the mass of warmed water from the volume of water and its density of 1025 kg/m. Then use the fact that 1 kcal of energy raises 1 kg of water by 10 and that the water warms by 25C. m V=At=- m = pAt = (1025 kg/m)(1.0 m)(0.510 m) = 0.5125 kg (1 kcal) (0.5125 kg)(25 C). (1 kg)(1 C) = 12.8 kcal; 12.8 kcal 1 bar 300 kcal = 0.043 bars 0.04 bars 4.186103 J 4. (a) 2500 Cal 1.0107 J 1 Cal 1 kWh (b) 2500 Cal 2.9 kWh 860 Cal (c) At 10 cents per day, the food energy costs $0.29 per day. It would be impossible to feed yourself in the United States on this amount of money. 6. The energy generated by using the brakes must equal the car's initial kinetic energy, since its final kinetic energy is 0. = Q=mv (1300 kg) (95 km/h) 1 m/s 3.6 km/h =4.526104 J=4.5104 J 4.526104 J 1 kcal 4186 J =108.1 kcal 110 kcal 7. The energy input is causing a certain rise in temperature, which can be expressed as a number of joules per hour per Co. Convert that to mass using the definition of kcal, relates mass to heat energy. 3.2107 J/h 1 kcal (1 kg)(1 C) = 254.8 kg/h = =250 kg/h 8. 9. 30 C 4186 J 1 kcal The wattage rating is 375 joules per second. Note that 1 L of water has a mass of 1 kg. (2.5x10 L) (60 C) 1 kg 1L 1 kcal 4186 J (1 kg)(1 C) kcal 1s 375 J =167 s 170 s = 2.8 min The heat absorbed can be calculated from Eq. 14-2. Note that 1 L of water has a mass of 1 kg. Q=mcAT (18L) 1x10-3 m 1.010 kg 1 m 1L |(4186 J/kg C)(95C-15C) = 6.0106 J 10. The specific heat can be calculated from Eq. 142. Q=mcAT C= 1.35105 J =1715 J/kg C 1700 J/kg. C =2 Q MAT (4.1 kg)(37.2C-18.0C) 11. (a) The heat absorbed can be calculated from Eq. 14-2. Note that 1 L of water has a mass of 1 kg. 1103 m Q=mcAT = (1.0 L)| 1 L 1.010 kg 1 m (4186 J/kg. C)(100C -20C) =3.349105 J= 3.3105 (b) Power is the rate of energy usage. 3.349105 J P = At= =5582 s 5600 s 93 min At P 60 W 14. The heat lost by the copper must be equal to the heat gained by the aluminum and the water. The aluminum and water have the same temperature change. mcucu (Ticu-Teq)=MAICA (Teq-T)+"HOCHO (Tea - THO) [(0.145 kg)(900 J/kg.C) (0.265 kg)(390 J/kg. C)(245C Teq) =| + (0.825 kg)(4186 J/kg. ()] (Tea - (Teq -12.0C) Teq=18.532C 18.5C 15. The heat gained by the glass thermometer must be equal to the heat lost by the water. mglass glass (Teq-glass) = "HOCHO (THO-Teq) (31.5 g)(0.20 cal/gC)(41.8C 23.6C) = (135 g)(1.00 cal/g C)(0 41.8C) TH,O =|42.6C| 17. The heat lost by the iron must be the heat gained by the aluminum and the glycerin. mFe CFe (TiFe -Teq) = mA1CA1 (Teq - Ti A1) +mglyCgly (Teq Tigly) 18. (a) 19. (0.290 kg)(450 J/kg C)(142 C) = (0.095 kg)(900 J/kg. C)(28 C)+(0.250 kg)cly (28 C) Cgly = 2305 J/kg C 2300 J/kg C Since Q=mcAT and Q = CAT, equate these two expressions for Q and solve for C. C = mc Q=mcAT CAT (b) For 1.0 kg of water: (c) For 45 kg of water: C=mc = (1.0 kg)(4186 J/kg C) = 4.210 J/C| C = mc = (45 kg)(4186 J/kg. C) = 1.9105 J/C We assume that all of the kinetic energy of the hammer goes into heating the nail. 8 (1" hammer hammer) = mnail Fe AT KE = =Q AT = 2 8(" hammer | hammer mnail Fe 4(1.20 kg)(7.5m/s) (0.014 kg)(450 J/kg. C) = 42.86 C 43 Co 20. 20 The heat lost by the substance must be equal to the heat gained by the aluminum, water, and glass. mxCx (Tix Teq) = MAICA (Teq - Ti A1) +mHOCHO (Teq TiHO) + Mglass glass (Teq - Tiglass) Cx = - - - MAICA(Teq A)+HOCHO (Teq THO) +mglass glass (Teq Tiglass ) mx (Tix - Teq) (0.105 kg)(900 J/kg. C) + (0.185 kg)(4186 J/kg C)] (35.0C-10.5C) +(0.017 kg)(840 J/kg. C) (0.215 kg)(330C-35.0C) 21 21. = 341.16 J/kg. Co= 341 J/kg C 65% of the original potential energy of the aluminum goes to heating the aluminum. 0.65 PEQ AT = 0.65mA1gh = MAICAI AT 0.65 gh 0.65(9.80 m/s)(55 m) (900 J/kg. C) CA1 = 0.39 C 24. 24 25. The oxygen is all at the boiling point, so any heat added will cause oxygen to evaporate (as opposed to raising its temperature). We assume that all the heat goes to the oxygen and none to the flask. 26. Q Q=mLy m = Lv 3.40105 J 2.1105 J/kg = 1.6 kg The silver must be heated to the melting temperature and then melted. Q=Qheat+melt = mcAT +mLF = (23.50 kg)(230 J/kg. C)(961C -25C)+(23.50 kg)(0.88105 J/kg) = 7.1106 J Assume that the heat from the person is only used to evaporate the water. Also, we use the heat of vaporization at room temperature (585 kcal/kg), since the person's temperature is closer to room temperature than 100C. 27. Q = mLy m = Lv 185 kcal 585 kcal/kg = |0.316 kg = 316 mL The heat lost by the steam condensing and then cooling to 30C must be equal to the heat gained by the ice melting and then warming to 30C. m "steam [LV + CHO (Tisteam - Teq)] = mice [LF + CHO (Teq - Tiice )] m. steam = mice [LE + CHO (Teq - Tice)] -Teq)] [Ly +CHO (Tisteam = 0.18 kg = (1.00 kg): [3.3310 J/kg+(4186 J/kg. C)(30C)] [22.610 J/kg+(4186 J/kg C)(30C)]