SOLVE PART C: LOSS OF GOODWILL: I need help solving this problem using the solver, I need to use these values to get the additional cost of customer goodwill, I know the ANSWER IS $8.70 but HOW do I use the excel solver to get that answer?

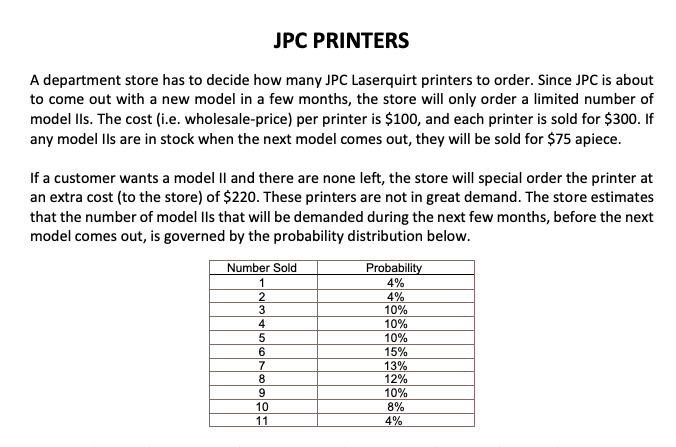
JPC PRINTERS A department store has to decide how many JPC Laserquirt printers to order. Since JPC is about to come out with a new model in a few months, the store will only order a limited number of model lls. The cost (i.e. wholesale-price) per printer is $100, and each printer is sold for $300. If any model Ils are in stock when the next model comes out, they will be sold for $75 apiece. If a customer wants a model II and there are none left, the store will special order the printer at an extra cost (to the store) of $220. These printers are not in great demand. The store estimates that the number of model lls that will be demanded during the next few months, before the next model comes out, is governed by the probability distribution below. Number Sold 1 2 3 4 5 6 7 8 9 10 11 Probability 4% 4% 10% 10% 10% 15% 13% 12% 10% 8% 4% The store manager thinks that the cost when they run short of model II printers should include an additional cost for lost customer goodwill each time a customer makes the trip to the store and goes empty-handed. How high would this loss of goodwill cost have to be before the retail store orders one more of these printers than was found in part (b)? Use Excel Solver for this purpose. Inputs $400 $150 Regular selling price, Initial cost from the supplier, c1 Discounted price when next model comes out, s Extra cost from the supplier, c2 $100 $200 Probability distribution of demand b. k 1 2 3 4 5 7 8 4 9 10 11 6 0.15 0.04 0.04 0.1 0.1 0.1 0.13 0.12 0.1 0.08 0.04 P(D=K) FD(K) 0.04 0.08 0.18 0.28 0.38 0.53 0.66 0.78 0.88 0.96 1 a. Understocking cost (unit Cu) Overstocking cost (unit Co) Critical Ratio $50 $50 0.50 Cu/(Curco) We see that Q=6 is optimal. In order to gather this information I looked a the chart finding what was less than the close to the critical ration but would capitalize on what was needed. EXPECTED DEMAND 6.23 About 6 units Part C. Critical Ratio application is needed = 0.54 0.53 critical ratio is used because it asked what the high loss would be in part b which was 6 So, we use CUMULATIVE DISTRIBUTION FUNCTION of 0.53 to have the NEXT QUANTITY OF 6. Loss of goodwill cost c. Understocking cost Overstocking cost Critical Ratio $58.70 $50 0.54 Part C. Critical Ratio application is needed = 0.54 0.53 critical ratio is used because it asked what the high loss would be in part b which was 6 So, we use CUMULATIVE DISTRIBUTION FUNCTION of 0.53 to have the NEXT QUANTITY OF 6. Loss of goodwill cost Understocking cost Overstocking cost Critical Ratio $58.70 $50 0.54 JPC PRINTERS A department store has to decide how many JPC Laserquirt printers to order. Since JPC is about to come out with a new model in a few months, the store will only order a limited number of model lls. The cost (i.e. wholesale-price) per printer is $100, and each printer is sold for $300. If any model Ils are in stock when the next model comes out, they will be sold for $75 apiece. If a customer wants a model II and there are none left, the store will special order the printer at an extra cost (to the store) of $220. These printers are not in great demand. The store estimates that the number of model lls that will be demanded during the next few months, before the next model comes out, is governed by the probability distribution below. Number Sold 1 2 3 4 5 6 7 8 9 10 11 Probability 4% 4% 10% 10% 10% 15% 13% 12% 10% 8% 4% The store manager thinks that the cost when they run short of model II printers should include an additional cost for lost customer goodwill each time a customer makes the trip to the store and goes empty-handed. How high would this loss of goodwill cost have to be before the retail store orders one more of these printers than was found in part (b)? Use Excel Solver for this purpose. Inputs $400 $150 Regular selling price, Initial cost from the supplier, c1 Discounted price when next model comes out, s Extra cost from the supplier, c2 $100 $200 Probability distribution of demand b. k 1 2 3 4 5 7 8 4 9 10 11 6 0.15 0.04 0.04 0.1 0.1 0.1 0.13 0.12 0.1 0.08 0.04 P(D=K) FD(K) 0.04 0.08 0.18 0.28 0.38 0.53 0.66 0.78 0.88 0.96 1 a. Understocking cost (unit Cu) Overstocking cost (unit Co) Critical Ratio $50 $50 0.50 Cu/(Curco) We see that Q=6 is optimal. In order to gather this information I looked a the chart finding what was less than the close to the critical ration but would capitalize on what was needed. EXPECTED DEMAND 6.23 About 6 units Part C. Critical Ratio application is needed = 0.54 0.53 critical ratio is used because it asked what the high loss would be in part b which was 6 So, we use CUMULATIVE DISTRIBUTION FUNCTION of 0.53 to have the NEXT QUANTITY OF 6. Loss of goodwill cost c. Understocking cost Overstocking cost Critical Ratio $58.70 $50 0.54 Part C. Critical Ratio application is needed = 0.54 0.53 critical ratio is used because it asked what the high loss would be in part b which was 6 So, we use CUMULATIVE DISTRIBUTION FUNCTION of 0.53 to have the NEXT QUANTITY OF 6. Loss of goodwill cost Understocking cost Overstocking cost Critical Ratio $58.70 $50 0.54