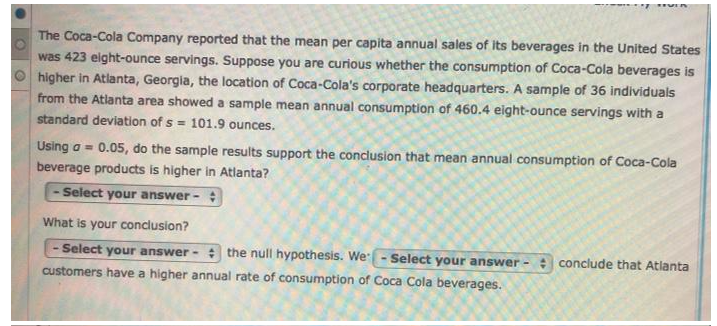
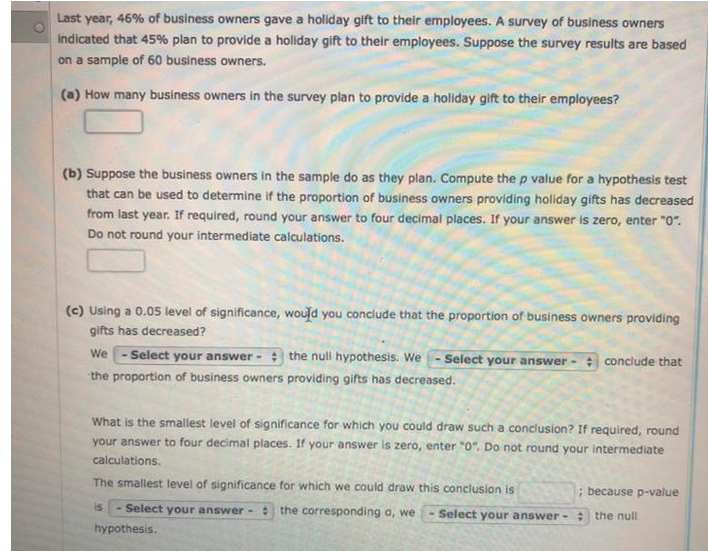
,. solve please

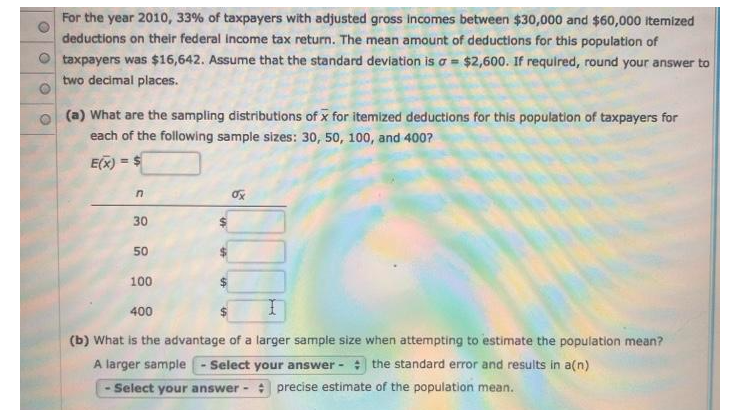
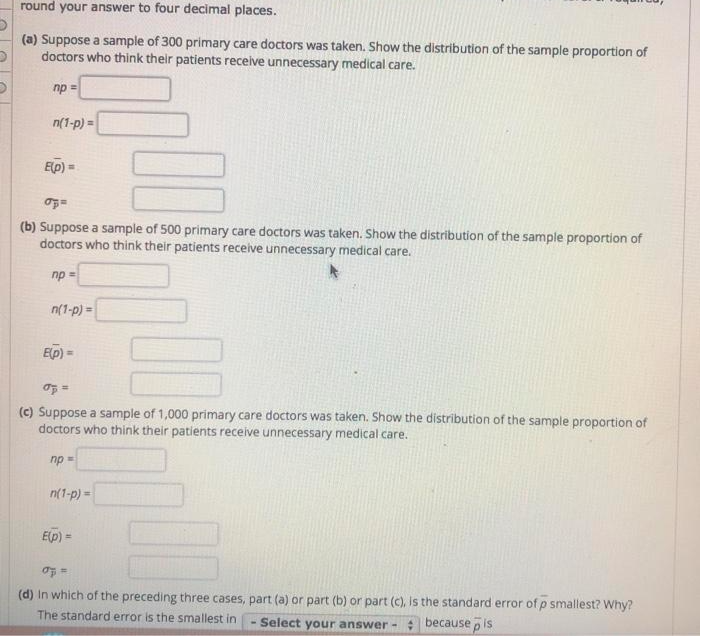
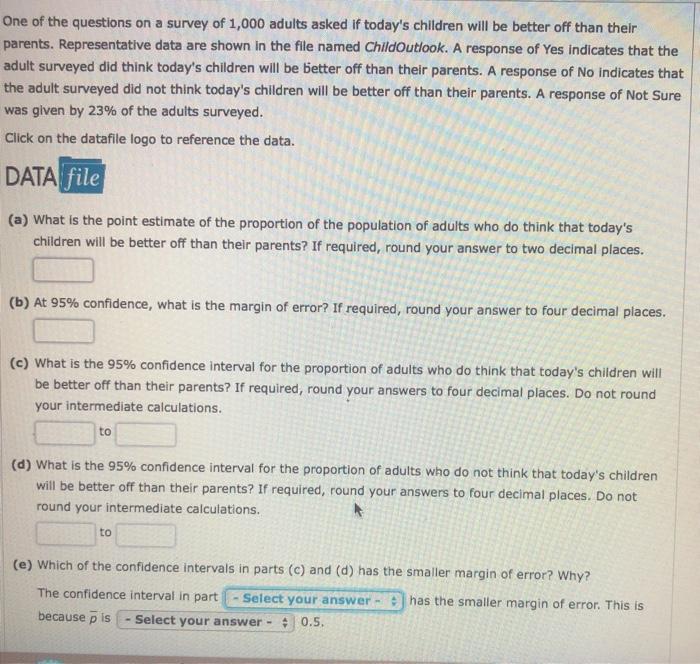
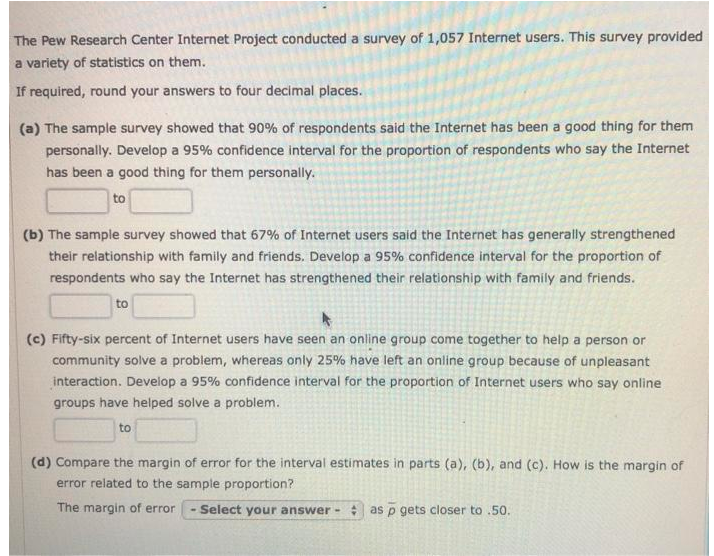
For the year 2010, 33% of taxpayers with adjusted gross incomes between $30,000 and $60,000 itemized O deductions on their federal Income tax return. The mean amount of deductions for this population of O taxpayers was $16,642. Assume that the standard deviation is a = $2,600. If required, round your answer to two decimal places. (a) What are the sampling distributions of x for itemized deductions for this population of taxpayers for each of the following sample sizes: 30, 50, 100, and 400? E(x) = n 30 50 100 400 (b) What is the advantage of a larger sample size when attempting to estimate the population mean? A larger sample - Select your answer - : the standard error and results in a(n) - Select your answer - * precise estimate of the population mean.round your answer to four decimal places. (a) Suppose a sample of 300 primary care doctors was taken. Show the distribution of the sample proportion of doctors who think their patients receive unnecessary medical care. np = n(1-p) = E(p) = (b) Suppose a sample of 500 primary care doctors was taken. Show the distribution of the sample proportion of doctors who think their patients receive unnecessary medical care. np = n(1-p) = E(p) = (c) Suppose a sample of 1,000 primary care doctors was taken. Show the distribution of the sample proportion of doctors who think their patients receive unnecessary medical care. np = n(1-p) = E(p) = (d) In which of the preceding three cases, part (a) or part (b) or part (c), Is the standard error of p smallest? Why? The standard error is the smallest in | - Select your answer - : because , isOne of the questions on a survey of 1,000 adults asked if today's children will be better off than their parents. Representative data are shown In the file named ChildOutlook. A response of Yes indicates that the adult surveyed did think today's children will be better off than their parents. A response of No indicates that the adult surveyed did not think today's children will be better off than their parents. A response of Not Sure was given by 23% of the adults surveyed. Click on the datafile logo to reference the data. DATA file (a) What is the point estimate of the proportion of the population of adults who do think that today's children will be better off than their parents? If required, round your answer to two decimal places. (b) At 95% confidence, what is the margin of error? If required, round your answer to four decimal places. (c) What is the 95% confidence interval for the proportion of adults who do think that today's children will be better off than their parents? If required, round your answers to four decimal places. Do not round your intermediate calculations. to (d) What is the 95% confidence interval for the proportion of adults who do not think that today's children will be better off than their parents? If required, round your answers to four decimal places. Do not round your intermediate calculations. to (e) Which of the confidence intervals in parts (c) and (d) has the smaller margin of error? Why? The confidence interval in part - Select your answer - : | has the smaller margin of error. This is because p is- Select your answer - + 0.5.The Pew Research Center Internet Project conducted a survey of 1,057 Internet users. This survey provided a variety of statistics on them. If required, round your answers to four decimal places. (a) The sample survey showed that 90% of respondents said the Internet has been a good thing for them personally. Develop a 95% confidence interval for the proportion of respondents who say the Internet has been a good thing for them personally. to (b) The sample survey showed that 67% of Internet users said the Internet has generally strengthened their relationship with family and friends. Develop a 95% confidence interval for the proportion of respondents who say the Internet has strengthened their relationship with family and friends. to (c) Fifty-six percent of Internet users have seen an online group come together to help a person or community solve a problem, whereas only 25% have left an online group because of unpleasant interaction. Develop a 95% confidence interval for the proportion of Internet users who say online groups have helped solve a problem. to (d) Compare the margin of error for the interval estimates in parts (a), (b), and (c). How is the margin of error related to the sample proportion? The margin of error | - Select your answer - : as p gets closer to .50.\fLast year, 46% of business owners gave a holiday gift to their employees. A survey of business owners Indicated that 45% plan to provide a holiday gift to their employees. Suppose the survey results are based on a sample of 60 business owners. (a) How many business owners in the survey plan to provide a holiday gift to their employees? (b) Suppose the business owners in the sample do as they plan. Compute the p value for a hypothesis test that can be used to determine if the proportion of business owners providing holiday gifts has decreased from last year. If required, round your answer to four decimal places. If your answer is zero, enter "0". Do not round your intermediate calculations. (c) Using a 0.05 level of significance, would you conclude that the proportion of business owners providing gifts has decreased? We - Select your answer - * the null hypothesis. We - Select your answer - * conclude that the proportion of business owners providing gifts has decreased. What is the smallest level of significance for which you could draw such a conclusion? If required, round your answer to four decimal places. If your answer is zero, enter "0". Do not round your intermediate calculations. The smallest level of significance for which we could draw this conclusion Is ; because p-value is - Select your answer - : |the corresponding o, we - Select your answer - : the null hypothesis.A researcher has data on class size (CS) and average test scores from 100 econometrics classes (TS). He estimates the OLS regression and obtains the following regression line: TS = 520.4-5.82 x CS reg (20.4) (2.21) where the R2 = 0.08, SER = 11.5, and the standard errors of each coefficient is in parentheses underneath. inf a) What are Bo and B1, and what are their standard errors? 51 b) Interpret the R for this regression. c) A classroom has 22 students. What is the regression's prediction for that classroom's average test score? d) Last year a classroom had 19 students and this year it has 23 students. What is the regression's prediction for the change in the classroom average test score? (Hint: A change of 1 unit of X induces a change of B 1 units in Y, so a change in 4 units of X will induce what change in Y?) e) The sample average class size across the 100 classrooms is 21.4. What is the sample average of test scores across the 100 classrooms? (Hint: The estimated regression line (above) gives you the average relationship between Y and X!) f) Is Bi significant at the 5% significance level (i.e. can you reject the null that B 1 = 0)? (Hint: Same procedure as 4b where the critical value is now for 98 degrees of freedom at the 5% level-see Table 2) . g) Construct a 95% confidence interval for 1, the regression slope coefficient.3. An economics department at a large state university keeps track of its majors' starting salaries. Does taking econometrics affect starting salary? Let SAL = salary in dollars, GPA = grade point average on a 4.0 scale, METRICS = 1 if student took econometrics, and METRICS = 0 otherwise. Using the data file metrics.dat, which contains information on 50 recent graduates, we obtain the estimated regression SAL = 24200 + 1643GPA + 5033METRICS R= = 0.74 (se ) (1078) (352) (456) (a) Interpret the estimated equation. (b) How would you modify the equation to see whether women had lower starting salaries than men? (Hint: Define an indicator variable FEMALE = 1, if female; zero otherwise.) (c) How would you modify the equation to see if the value of econometrics was the same for men and women?1. Consider the simple regression model: Vi = Bo+ Biri + Hi, for i = 1, ... . n, with E(uilz,) - 0 and let a be a dummy instrumental variable for I, such that we can write: Ci =not matu with E(uilz;) = 0 and E(viz) =0. (c) Denote by no, the number of observations for which = = 0 and by n, the number of observations for which a, = 1. Show that: (a - 2) = =(n-m). 1=1 and that: [( - =)(y: - 9) = -(n - n) (31 - 30) . where to and g are the sample means of y for z equal to 0 and 1 respectively. ( Hint: Use the fact that n = nj + no, and that = = m). (d) Now we regress y on i to obtain an estimator of &. From the standard formula of the slope estimator for an OLS regression and using the result in (c), show that: B - 91 -90 $1 - To This estimator is called the Wald estimator.