
Solve problems 6,7,8,9, and 10 for me please.
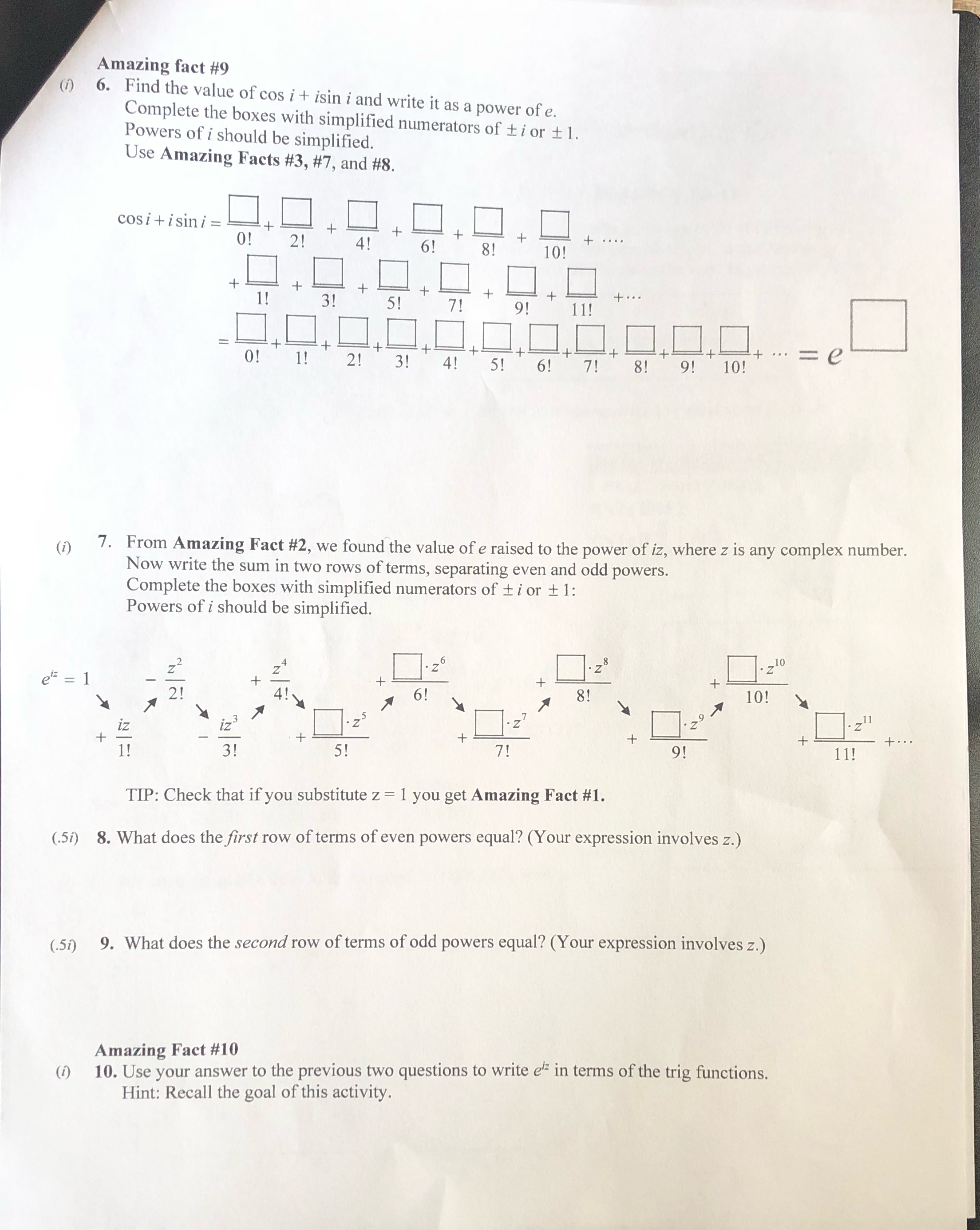
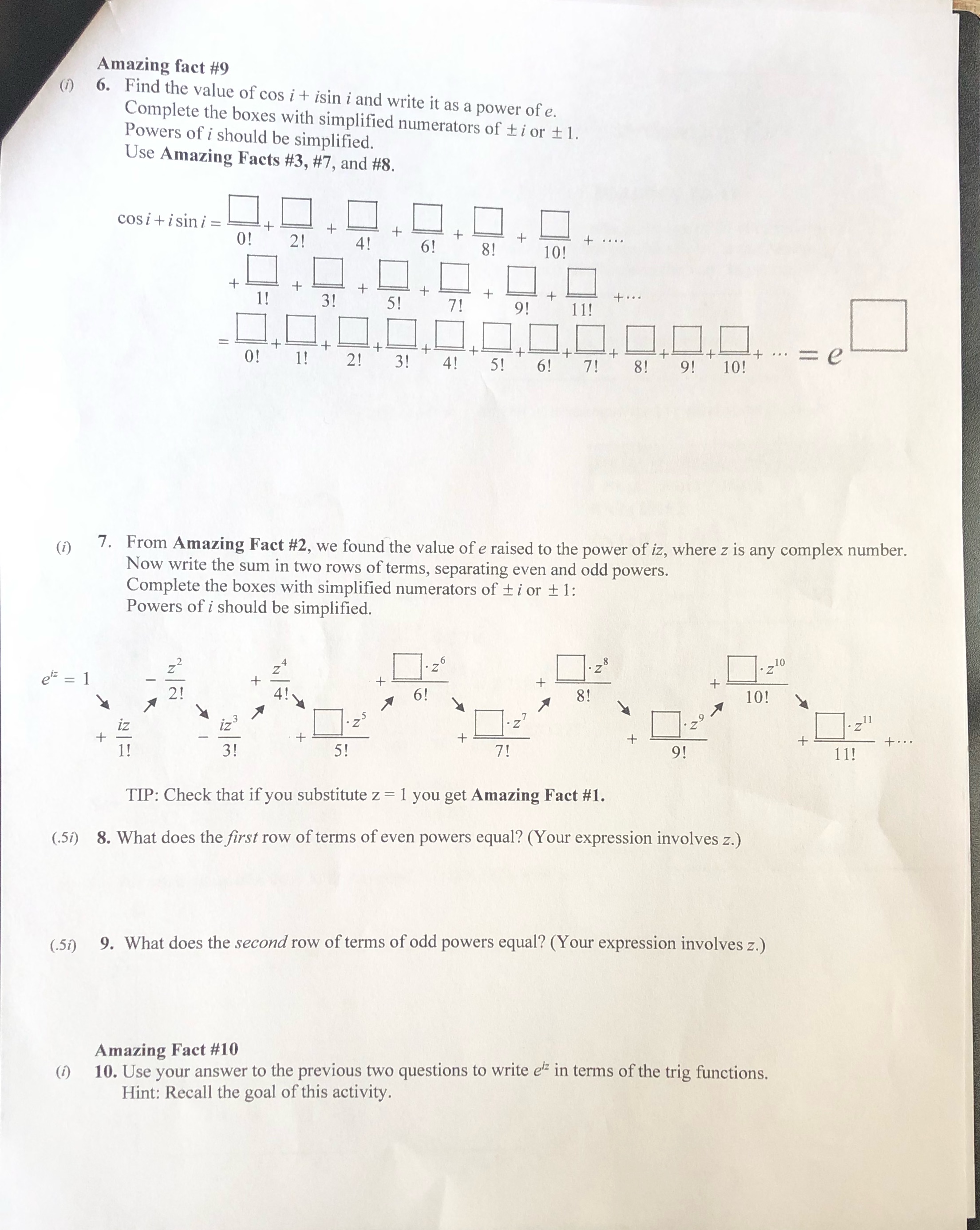
Amazing fact #9 (i) 6. Find the value of cos i + isin i and write it as a power of e. Complete the boxes with simplified numerators of ti or + 1. Powers of i should be simplified. Use Amazing Facts #3, #7, and #8. cosi + isin i = 21 41 101 -+ 31 11 2! 3! 4! . = e 5! 6! 7! 8! 9! 10! (i) 7. From Amazing Fact #2, we found the value of e raised to the power of iz, where z is any complex number. Now write the sum in two rows of terms, separating even and odd powers. Complete the boxes with simplified numerators of ti or + 1: Powers of i should be simplified. . Z 210 p /z 21 81 10! 1.29 N IZ + 1 ! 3 ! + + ... 5! 7! 91 11! TIP: Check that if you substitute z = 1 you get Amazing Fact #1. (.57) 8. What does the first row of terms of even powers equal? (Your expression involves z.) (.51) 9. What does the second row of terms of odd powers equal? (Your expression involves z.) Amazing Fact #10 (i) 10. Use your answer to the previous two questions to write e in terms of the trig functions. Hint: Recall the goal of this activity.series 1 + 1! 21 31 4! + ...= e Notice this equation is true for w = 0 since e" = 1 and 1 + 0 + 0 +0+ ... =1. Notice this holds for w = 1 by Amazing Fact #1. Amazing Fact #3 (1) 2. Suppose w = -1 in Amazing Fact #2. Write the first thirteen terms of the infinite series expansion of e raised to the power of -1. Powers of i should be simplified. Double check you only report thirteen terms. O ! +1 1! + 2! 31 4! -51 + 6! -717 8! -9! +70! 711 +121 Amazing Fact #4 (1) 3. If w = i in Amazing Fact #2, then e' = f+ +2 PPP PPP P1 21 31 41 51 + 61 + 71 + 81+ 1 12 91 7 101 11! 12 ! + ...... We can simplify this just a little using powers of i, where ?? = -1, i = -i, etc. Rewrite the expansion with simplified numerators of i or + 1, by carefully completing the boxes below. e'= 1 - i 1 i 0! 1! 2! 3 ! 4! 1 1 1 4 1 1 - 1 1 5 ! 6! 7 ! + ...... 8 ! 9! 10! 11! 12! (1) 4. Suppose w = iz in Amazing Fact #2, where z is any complex number. Write the first thirteen terms of the infinite series expansion of e raised to the power of iz. Powers of i should be simplified. Double check you only report thirteen terms. 0 ! 1! 2! 34 4! ! 61 71 + 87 + 12 - 2 - 121 72 1 Amazing fact #5 If w is any complex number in radians, the infinite series 1 W 2 w 4 W6 O! WB W10 2 ! W 12 W 14 4 ! 6 ! 8 ! 10 ! 12! 14! + ... = Cosw Notice this is true for w = 0 since cos 0 = 1 - 0 +0-0+ ... =1 Amazing fact #6 If w is any complex number in radians, the infinite series w w ? w' will W 13 wis 1 ! 3 ! 5 ! 7! 9 ! 11! 13! 15! + ... = sin w Notice this is true for w = 0 since sin 0 = 0 -0 +0-0+ ... =0 Amazing facts #7 and #8 (21) 5. Complete the boxes with simplified numerators of ti or + 1 to find the value of sin i and cos i. Powers of i should be simplified. cosi = -1 O ! 2! 4! 6! 8! 10! sin i = +.... =i 1! 3! 5! 7! 9 ! 11! 1! 3! 5 ! 7 ! 9 ! 11