Solve the following attachments
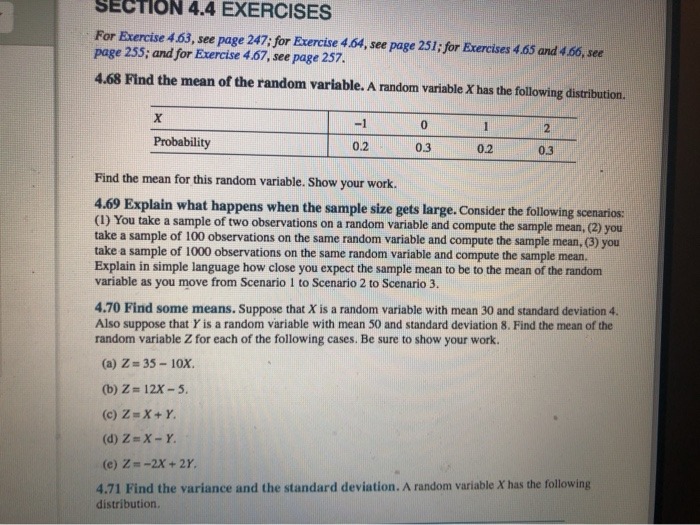
(3-) Suppose the effort level chosen by the agent is observable by the principal. A wage contract then species an effort level (61 or cg), and an outputcontingent wage schedule {u-'H, mg}. Here 11);; is the wage paid if the project yields 8, and am is the wage paid if the project yields 0. If effort is observable, it is optimal for the principal to choose a xed wage contract (that is? set *wH = TEL) for each effort level. Informally1 explain the intuition for this result. If effort is observable, which effort level should the principal implement? What is the best wage contract that implements this effort? If effort is not observable: which effort level should the principal implement? What is the best wage contract that implements this effort? Consider a situation in which a risk-neutral principal wishes to contract an agent to work on a project. The project produces output x = e + $ where e is the agent's effort and & is a normally distributed random variable with mean 0 and variance 1 (that is, & ~ N(0, 1)). The agent's utility of wealth function is u(w) = E(w) -2Var(w) where E is expectation and Var is variance. The agent's disutility of effort function is v(e) = 0.5e- and his reservation utility is u = 0. The principal can only offer contracts with the form w= a + Bx a) Show that the agent's expected utility from a contract can be written as a + Be - 282 - 0.5e2. b) Show that the principal's expected utility from a contract can be written as (1 - B)e - a c) Write the principal's maximization problem when effort is verifiable. d) When effort is verifiable, what are the optimal values for a and B for the principal? e) When effort is verifiable, what effort level does the principal contract the agent to exert? f) Write the principal's maximization problem when effort is unverifiable. Why is it different from the maximization problem with verifiable effort?SECTION 4.4 EXERCISES For Exercise 4.63, see page 247; for Exercise 4.64, see page 251; for Exercises 4.65 and 4 60, see page 255; and for Exercise 4.67, see page 257. 4.68 Find the mean of the random variable. A random variable X has the following distribution. X -1 0 2 Probability 0.2 0.3 0.2 0.3 Find the mean for this random variable. Show your work. 4.69 Explain what happens when the sample size gets large. Consider the following scenarios: (1) You take a sample of two observations on a random variable and compute the sample mean, (2) you take a sample of 100 observations on the same random variable and compute the sample mean, (3) you take a sample of 1000 observations on the same random variable and compute the sample mean. Explain in simple language how close you expect the sample mean to be to the mean of the random variable as you move from Scenario 1 to Scenario 2 to Scenario 3. 4.70 Find some means. Suppose that X is a random variable with mean 30 and standard deviation 4. Also suppose that Y is a random variable with mean 50 and standard deviation 8. Find the mean of the random variable Z for each of the following cases. Be sure to show your work. (a) Z = 35 - 10X. (b) Z = 12X - 5. (c) Z=X+Y. (d) Z=X-Y. (e) Z= -2X + 27. 4.71 Find the variance and the standard deviation. A random variable X has the following distribution.Consider the model below describing the supply and demand for bananas. Q5 = Bo + BB+ US (1) Q? = Qo + mili+ Up (2) P; is the price of banana, Q; is the supply of banana, @? is the demand of banana. UP and UP are mutually independent IID random variables with a mean of zero, and variances equal to o?, and of, respectively. Of = QP is the market equilibrium condition. (a) Show that P, and UP are correlated. (15 points) (b) Show that the OLS estimator of on is biased. (5 points) Now, We add a new explanatory variable Y, into the demand function of banana. Y, describes the income level and is exogenous which means Y is uncorrelated with both UP and US. Of = Bo + BIR:+ US (3) Q? = an+ on Pi + 02Vi+ UP (4) (c) With equation (3) (4) and the market equilibrium condition, write Q = ng+ xiY, +e;. Find ag, x1, and e; as functions of Bo, 81, 00, 01, 02, US, and UP. (10 points)