




,solve the following
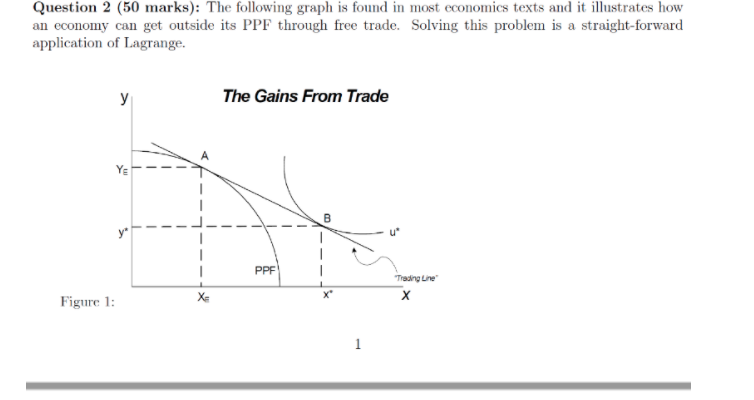
Consider a twoperiod model of a small open economy with a single good each period and no investment. Let preferences ofthe representative household be described by the utility function urc1,c21 = {C1 + pic: The parameter IE is known as the subjective discourrt factor. It measures the consumer's degree of impatience in the sense that the smaller ,3 is, the higher is the weight the consumer assigns to present consumption relative to future consumption. Assume that ,8 = 1!].1. The representative household has initial net foreign wealth of {1 + r0} EN] = 1, with r = :11, and is endowed with 01 = 5 units of goods in period 1 and 02 = ID units in period lThe world irrterest rate paid on assets held from period lto period 2, r*, equals 10% {r* = :11] and there is free international capital mobility. 1. Calculate the equilibrium levels of C1, C2, 1131, CA1. 2. Suppose now that the government imposes capital corrtrols that require that the country's net foreign asset position at the end of period 1 be nonnegative [Fl 2 ID]. Compute the equilibrium value of the domestic interest rate r1, C1, C2,TB]_, CA1. 3. Evaluate the effect of capital corrtrols on welfare. Specically, nd the level of utility under capital controls and compare it to the level of utility obtained under free capital mobility. :Capital controls] Consider a two-period model of a small open economy-with a single good- each period and no investment. Let preferences of the representative household he described by the utilitv function: UIIchcg} = vii-3+ v where 3 denotes the subjective discount factor. Assume that :3: . The representative house hold has initial net foreign wealth of {l + rulBg = 1. wither: = Ill. and is entimi'ed with tn = 5 units of goods in period 1 and if; 2 it] units in period 2-. The vvorid interest rate paid on assets held from period He period 2. 1*, equals \"1% {i.e.. vs: 11.1} and there is-iree international capital mobility. Calculate the equilibrium levels of consumption in period 1. c1. consumption in period is.- ca. the trade balance in period lr to\" and the current account balance in period 1. ml. Suppose that the government imposes capital controls that require that the country's net i'oreign asset position at the mid of period 1 he u'onnegative {BI 33: [l]. IClonipute again 15.1, ca. 151 amt! m1 and evaluate the effect of capital cndtrols on welfare. Provide a brief economic interpretation [f your results. Hinder 1e'rhat circumstances would the capital controls not be binding? Expiin'without using any.r derivations. Question 1: Problem solving {Ill Marks) The Production Costi'canister {$) and the Weekly Sales 1'v'olume (number of canisters) of a variety of olive oil were recorded in a sample of 6 oil trading companies (table below): 011 Tradin Corn . Inn-nun _lm Weekl SalesVolume canistersxl Ill-m!\" 1. Construct a simple regression model to predict the Weekly Sales Volume by Production Coscanister. (4 Marks) 2. Find the predicted Weekly Sales Volume on that olive oil variety in an oil trading companyr where the Production Cost is $ SSI'canister. {I Mark) 3. Compute r2 and r forthis mode}. and interpret their values in this case. (3.5 Marina} 4. Calculate the prediction error for the "i'v'eeltljiF Sales Volume value of 600 canisters based on the regression model constructed previously. (1.5 Marks) Question 2 (50 marks): The following graph is found in most economics texts and it illustrates how an economy can get outside its PPF through free trade. Solving this problem is a straight-forward application of Lagrange. Skippy lives on a small island full of resources that lets her produce two goods: x and y. Her production possibility frontier (constraint) is given by x2 + y2 = 300. Skippy works alone to maximize her utility which is given by U(x; y) = x2y. (1) Set up the Lagrangian function for Skippy and solve for x and y. Use your solution to calculate U. (10 marks) (2) Carefully graph and label the PPF and Indifference Curve at the optimum. (10 marks) Now Skippy has the opportunity of trading in the world market. Skippy can trade whatever x and y she has at prices px and py. To maximize her gains from trade, Skippy needs to follow a 2-step process. Step 1. First, she maximizes her endowment position (maximize trading line) subject to her PPF, where the solution to this Lagrange problem (xE, yE) is her production decision and are her endowments she will use for trade. Step 2. Second, she maximizes utility subject to the constraint, pxxE + pyyE = pxx + pyy, where x and y are the quantities she trades for that maximize her utility. (3) If px = py = $1, please solve the Lagrangian that maximizes her endowments. Then use the endow- ment value and prices are given in the trading constraint to maximize her utility by the Lagrangian method. Calculate her utility number. (20 marks) (4) Give an economic interpretation to each Lagrangian multiplier in the endowment-maximization problem and the utility-maximization problem in (3). (10 marks)\fSkippy lives on a samll island full of resources that lets her produce two goods: r and y. Her production possibility frontier (constraint) is given by a2 + y' = 300. Skippy works alone to maximize her utility which is given by U(x, y) = xy. (1) Set up the Lagrangian function for Skippy and solve for r and y. Use your solution to calculate U. (10 marks) (2) Carefully graph and label the PPF and Indifference Curve at the optimum. (10 marks) Now Skippy has the opportunity of trading in the world market. Skippy can trade whatever r and y she has at prices pr and py. To maximize her gains from trade, Skippy needs to follow a 2-step process. Step 1. First, she maximizes her endowment position (maximize trading line) subject to her PPF, where the solution to this lagrange problem (XE, yE) is her production decision and are her endowments she will use for trade. Step 2. Second, she maximizes utility subject to the constraint, PETE + PyyE = Par* + pyy", where r* and y* are the quantities she trades for that maximize her utility. (3) If Pr = Py = $1, please solve the Lagrangian that maximizes her endowments. Then use the endow- ment value and prices given in the trading constraint to maximize her utility by the Lagrangian method. Calculate her utility number. (20 marks) (4) Give an economic intrepretation to each Lagrangian multiplier in the endowment-maximization problem and the utility-maximization problem in (3). (10 marks)


















