





,. solve the following
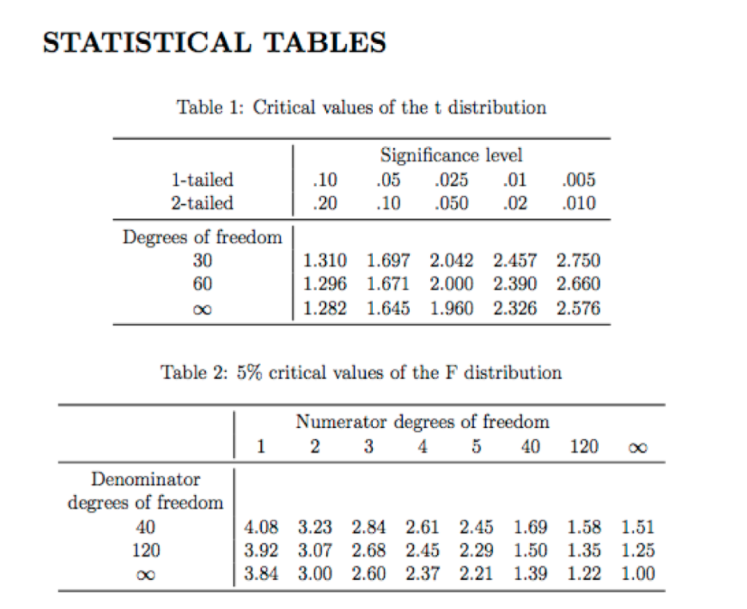
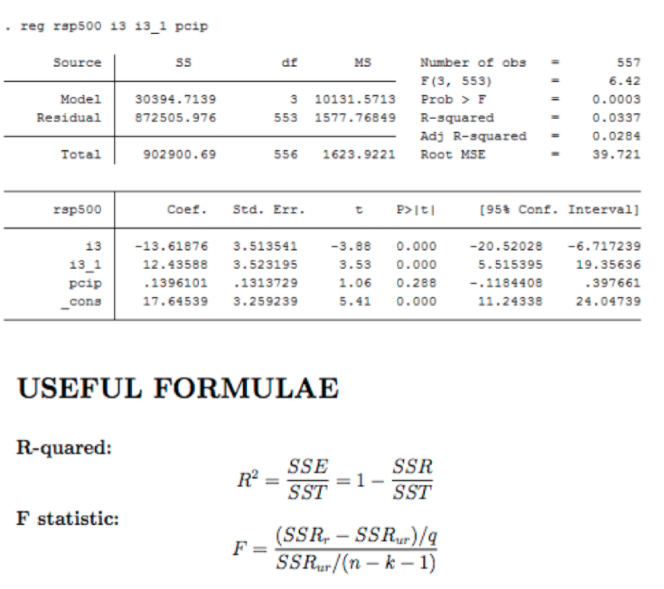
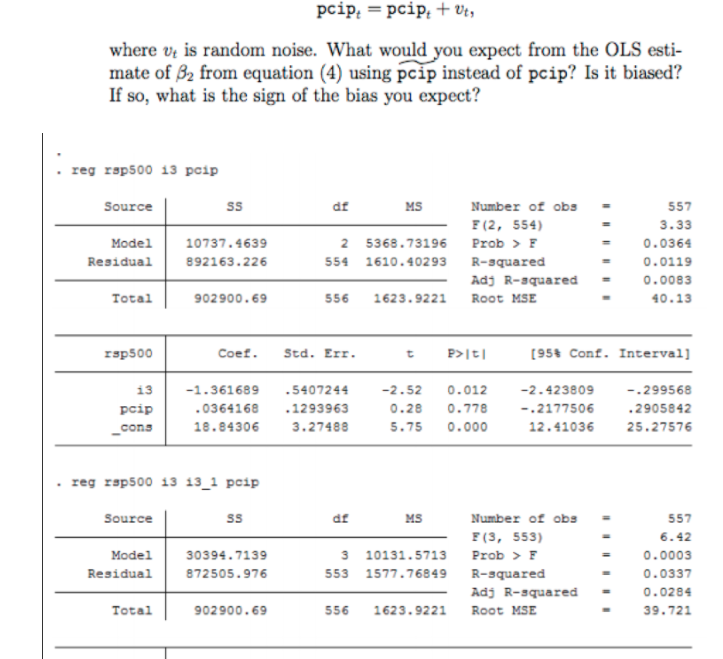
Consider the following models describing the relationship between monthly return on the Standard & Poor's 500 stock market index (rsp500), the re- turn on three-month T-bills (13) and the percentage change in industrial production (pcip): rsp500, = Bo+ 81i3, + Bopcip, + ut, (4) rsp500, = Bo + B1i3, + 8213t-1 + Bapcip, + ut. (5) 1. Is model (4) nested in the second model? If so, why? Which one appears to fit the data better? 2. Below are reported Stata outputs for OLS estimates of both models. Compare the estimated long-run propensity (LRP) for the effect of 13 derived from both models. Are they greatly different? 3. How would you rewrite the model (5) to directly estimate the LRP and its standard error? 4. Suppose the available information on pcip is a noisy measure of the true quantity, such that we only observe pcip, = pcip, + Ut,STATISTICAL TABLES Table 1: Critical values of the t distribution Significance level 1-tailed .10 .05 .025 .01 .005 2-tailed .20 .10 .050 .02 .010 Degrees of freedom 30 1.310 1.697 2.042 2.457 2.750 60 1.296 1.671 2.000 2.390 2.660 1.282 1.645 1.960 2.326 2.576 Table 2: 5% critical values of the F distribution Numerator degrees of freedom 2 3 4 5 40 120 Denominator degrees of freedom 40 4.08 3.23 2.84 2.61 2.45 1.69 1.58 1.51 120 3.92 3.07 2.68 2.45 2.29 1.50 1.35 1.25 3.84 3.00 2.60 2.37 2.21 1.39 1.22 1.00Question 4) Demand for Coffee (8 points/1 points each) Suppose you have the following estimated regressions for coffee consumption with 123 observations. Model1: C =2.43-1.22 P+ 2.35Y R= =0.48 (1.1) (0.18) (0.65) Model 2 : C =1.85-1.07 P+1.98Y +0.42 PT R= =0.59 (1.3) (0.13) (0.54) (0.16) Model 3:C =2.97-1.38P R= =0.39 (1.2) (0.13) Model 4:C =1.24-0.87 +1.48Y +0.32PT-0.18PM R' =0.60 (1.1) (0.20) (0.44) (0.13) 0.99 Where P is price index for coffee, Y represents the income index, PT is the price of tea, PM represents price of milk and C represents the cups of coffee consumed You are also given that C = 5, Y =1750, P = 8, PT =1.5, PM = 3.5. a) Consider Model 4, are these results consistent with economic theory? Explain your answer with statistical evidence. b) Can you test the overall significance for effects of price of coffee, income and price of tea on coffee demand? If YES, provide test result. If NO, explain your reasoning. c) Use an F-test approach to Test the following hypotheses. i) Price of milk and price of tea jointly affects the demand for coffee. ii) Income does not affect the demand for coffee. iii) Price of milk, income and price of tea jointly affects the demand for coffee. iv) Price of milk does not affect the demand for coffee. d) Do you agree with inclusion of price of milk in the regression estimations? Suggest other variables to be included in the demand line of coffee. Justify your answer. e) Is coffee an inferior good? Support your answer with statistical evidence. () Can you determine the price elasticity of demand for coffee? If YES, provide test result. If NO, explain your reasoning. g) Are coffee and tea substitutes? Support your answer with statistical evidence. h) Suppose that a researcher estimates Model I with a dependent variable of CT which is measured in 10 cups of coffee. Write down the results obtained by the researcher.1. Let V, W be a vector spaces and A e C(V, W). Definition : Let 7 be a subset of C(V). A subspace S of V is 7 - invariant iff T(S) CS VT ET. The vector space V is 7 - irreducible if the only 7 - invariant subspaces of V are trivial (either 0 or V). a. Let 7 be the subset of C(V) consisting of linear maps with rank 1. Show V is 7- irreducible. b. Let D e C(V) with TD = DT for all T E T with T as in part a. Show D is a scalar multiple of the identity map on V. (Hint: Consider matrix units E, & E T (wrt some B of V.)) c. Let T C C(V), SC C(W). Assume V is 7- irreducible, and W is S- irreducible and that the subsets AT = SA. Show either A = 0 or A is an isomorphism. 2. Let f, g ( F(x], and F a subfield of F1. If f | g in Fi[x] then f | g in F(x]. 3. Let V be a vector space over F. Let A e C(V). a. Show that if p E F[x] then p(A") = p(A)* as maps of C(V*). b. Show that if dim(V) = n is finite then the minimal polynomial of A is the minimal polynomial of A*. 4. Find the minimal and characteristic polynomials in R[x] for each of the following matrices A. 5. For each of the examples in question 1, state which A are diagonalizable in My(R), and find a matrix P so that PAP is diagonal for those that are. 6. a. Show that if NE C(VF) is nilpotent then op( N) = 0. (use 6d from last assignment). b. List the similarity classes of the (nonzero) nipotent linear maps of a 5 - dimensional vector space over F (i.e., give a representative matrix in each class).1. Let V be a complex inner product space. T: V - V is a linear operator. Assume that there exists a constant K > 0 such that [|T(v)||