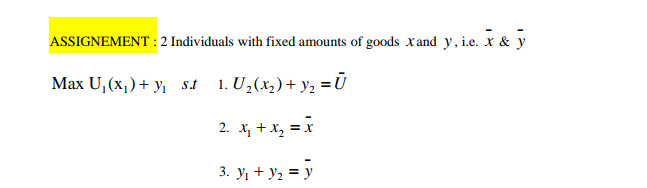Solve the following economics questions appropriately.

[8 points] Let the production function be Q (t) = f (t, K(t), L(t)) = exp (gt) K(t) "L(t ) 1-a, (1) where Q is total output, f (.) is the production function, K is capital input, L is labor input, and t is the time which indicates that the production function can shift over time due to technological changes. The notation exp (.) denotes the exponential function, g > 0 is a constant, and a E (0, 1) is the share of capital in the production function. Derive the expression of the growth rate of Q (t), i.e., dQ (t) dt Q (t) (2) in terms of the growth rates of capital and labor, dk (t) dL(t) and K (t) L(t) and two model parameters, o and g.ASSIGNEMENT : 2 Individuals with fixed amounts of goods Xand y, i.e. x & y Max U,(x, ) + y st 1.U2(x2 ) + y, = U 2. *+1=x 3. y + yz= yA life assurance company is examining the force of mortality, /x, of a particular group of policyholders. It is thought that it is related to the age, x, of the policyholders by the formula: Hx = Bc* It is decided to analyse this assumption by using the linear regression model: Y;= a+ Bxi+ E; where &; ~ N(0,o') are independently distributed The summary results for eight ages were as follows: Age, X 30 32 34 36 38 40 42 44 Force of mortality, 5.84 6.10 6.48 7.05 7.87 9.03 4, (x10 ) 10.56 12.66 In /, (3 s.f.) -7.45 -7.40 -7.34 -7.26 -7.15 -7.01 6.85 - 6.67 Ex, = 296 Ex, = 11,120 [In/x, =-57.129 > (In/, )? = 408.50 Ex, In/, =-2,104.5 (i) (a) Apply a transformation to the original formula, /, = Be , to make it suitable for analysis by linear regression. Hence, write down expressions for Y , o and B in terms of MY, B and c. (b) Plot a graph of In /, against the age of the policyholder, x. Hence comment on the suitability of the regression model and state how this supports your transformation in part (a). [4] (ii) Use the data to obtain least squares estimates of B and c in the original formula. [3] (iii) (a) Calculate the coefficient of determination between In /, and x. Hence comment on the fit of the model to the data. (b) Complete the table of residuals and use them to comment on the fit. [5] Age, X 30 32 34 36 38 40 42 44 Residual, 2; 0.08 -0.03 -0.06 0.02 0.09 (iv) Calculate a 95% confidence interval for the mean predicted response In //35 and hence obtain a 95% confidence interval for the mean predicted value of /35 . [4] [Total 16]