solve the question

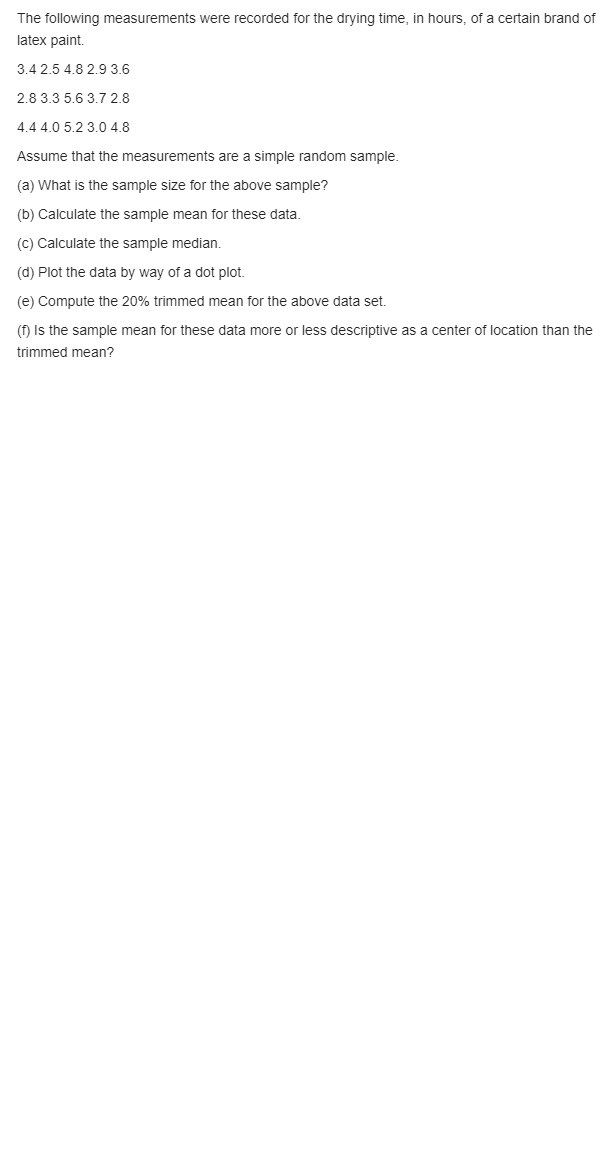
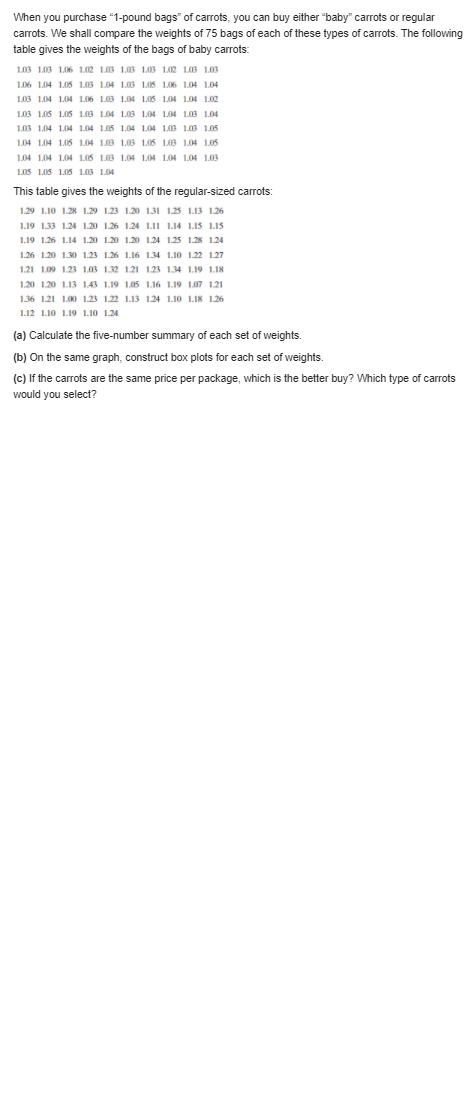
For the data of Exercise 1.4 on page 13, compute both the mean and the variance in "flexibility" for both company A and company B. Does there appear to be a difference in flexibility between company A and company B? Reference: Exercise 1.4: In a study conducted by the Department of Mechanical Engineering at Virginia Tech, the steel rods supplied by two different companies were compared. Ten sample springs were made out of the steel rods supplied by each company, and a measure of flexibility was recorded for each. The data are as follows: Company A: 9.3 8.8 6.8 8.7 8.5 6.7 8.0 6.5 9.27.0 Company B: 11.0 9.8 9.9 10.2 10.1 9.7 11.0 11.1 10.2 9.6 (a) Calculate the sample mean and median for the data for the two companies. (b) Plot the data for the two companies on the same line and give your impression regarding any apparent differences between the two companies.The following measurements were recorded for the drying time, in hours, of a certain brand of latex paint. 3.4 2.5 4.8 2.9 3.6 2.8 3.3 5.6 3.7 2.8 4.4 4.0 5.2 3.0 4.8 Assume that the measurements are a simple random sample. (a) What is the sample size for the above sample? (b) Calculate the sample mean for these data. (c) Calculate the sample median. (d) Plot the data by way of a dot plot. (e) Compute the 20% trimmed mean for the above data set. (f) Is the sample mean for these data more or less descriptive as a center of location than the trimmed mean?A new annular die process is to be installed for ex- truding pipes, tubes, and tubular films. The phase I installed price for the dies and machinery is $2,000,000. The manufacturer has not decided how to finance the system. The WACC over the last 5 years has averaged 10% per year. (a) Two financing alternatives have been de- fined. The first requires an investment of 40% equity funds at 9% and a loan for the balance at an interest rate of 10% per year. The second alternative requires only 25% cq- uity funds and the balance borrowed at 10.5% per year. Which approach will result in the smaller average cost of capital? (b) Yesterday, the corporate finance committee decided that the WACC for all new projects must not exceed the 5-year historical average of 10% per year. With this restriction, what is the maximum loan interest rate that can be in- curred for each of the financing alternatives?The initial cost of a bridge that is expected to be in place forever is $70 million. Maintenance can be done at 1-, 2-, 3-, or 4-year intervals, but the longer the interval between servicing, the higher the cost. The costs of servicing are estimated at $83,000, $91,000, $125,000, and $183,000 for intervals of 1 through 4 years, respectively. What interval should be scheduled for maintenance to minimize the overall equivalent annual cost? The interest rate is 8% per year. A construction company bought a 180,000 metric ton earth sifter at a cost of $65,000. The company expects to keep the equipment a maximum of 7 years. The operating cost is expected to follow the series described by 40,000 + 10,000k, where & is the number of years since it was purchased (* = 1, 2, . . ., 7). The salvage value is estimated to be $30,000 for years 1 and 2 and $20,000 for years 3 through 7. At an interest rate of 10% per year, deter- mine the economic service life and the associated equivalent annual cost of the sifter. An engineer determined the ESL of a new $80,000 piece of equipment and recorded the calculations shown below. [Note that the num- bers are annual worth values associated with various years of retention; that is, if the equip- ment is kept for, say, 3 years, the AW (years 1 through 3) of the first cost is $32,169, the AW of the operating cost is $51,000, and the AW of the salvage value is $6042.] The engineer forgot to enter the AW of the salvage value for 2 years of retention. From the information available, deter- mine the following: (a) The interest rate used in the ESL calculations. (b) The salvage value after 2 years, if the total AW of the equipment in year 2 was $78,762. Use the interest rate determined in part (a).The probability distribution of X, the number of imperfections per 10 meters of a synthetic fabric in continuous rolls of uniform width, is given by 1 2 3 I(x) 0.41 0.37 0.16 0.05 0.01 Construct the cumulative distribution function of X. Let X denote the diameter of an armored electric cable and Y denote the diameter of the ceramic mold that makes the cable. Both X and Y are scaled so that they range between 0 and 1. Suppose that X and Y have the joint density f (z, y) = - 01/2).The shelf life, in days, for bottles of a certain prescribed medicine is a random variable having the density function 20.000 f(x) = (x+100) I>0, 0 , elsewhere. Find the probability that a bottle of this medicine will have a shell life of (a) at least 200 days; (b) anywhere from 80 to 120 days.\f