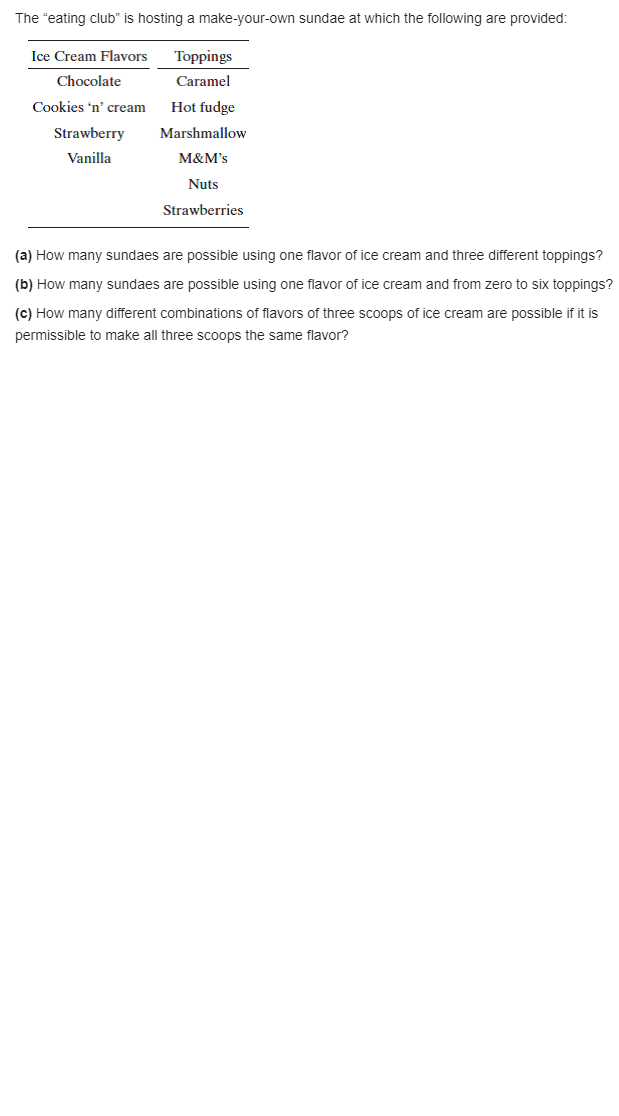
solve the question

Twenty adult males between the ages of 30 and 40 participated in a study to evaluate the effect of a specific health regimen involving diet and exercise on the blood cholesterol. Ten were randomly selected to be a control group, and ten others were assigned to take part in the regimen as the treatment group for a period of 6 months. The following data show the reduction in cholesterol experienced for the time period for the 20 subjects: Control group: 7 3 -4 14 2 522 -795 Treatment group: -6 5 9 4 4 12 37 5 3 3 (a) Do a dot plot of the data for both groups on the same graph. (b) Compute the mean, median, and 10% trimmed mean for both groups. (c) Explain why the difference in means suggests one conclusion about the effect of the regimen while the difference in medians or trimmed means suggests a different conclusion.In a study conducted by the Department of Mechanical Engineering at Virginia Tech, the steel rods supplied by two different companies were compared. Ten sample springs were made out of the steel rods supplied by each company, and a measure of flexibility was recorded for each. The data are as follows: Company A: 9.3 8.8 6.8 8.7 8.5 6.7 8.0 6.5 9.2 7.0 Company B: 11.0 9.8 9.9 10.2 10.1 9.7 11.0 11.1 10.2 9.6 (a) Calculate the sample mean and median for the data for the two companies. (b) Plot the data for the two companies on the same line and give your impression regarding any apparent differences between the two companies. An overseas shipment of 5 foreign automobiles contains 2 that have slight paint blemishes. If an agency receives 3 of these automobiles at random, list the elements of the sample space S, using the letters Band / for blemished and nonblemished, respectively; then to each sample point assign a value x of the random variable X representing the number of automobiles with paint blemishes purchased by the agency.A cereal manufacturer is aware that the weight of the product in the box varies slightly from box to box. In fact, considerable historical data have allowed the determination of the density function that describes the probability structure for the weight (inounces). Letting X be the random variable weight, in ounces, the density function can be described as (a) Verify that this is a valid density function. (b) Determine the probability that the weight is smaller than 24 ounces. (c) The company desires that the weight exceeding 26 ounces be an extremely rare occurrence. What is the probability that this rare occurrence does actually occur? A shipment of 7 television sets contains 2 defective sets. A hotel makes a random purchase of 3 of the sets. If x is the number of defective sets purchased by the hotel, find the probability distribution of X. Express the results graphically as a probability histogram.Consider the density function SAVE, 02, Y= 1); c) (C) P(X > Y);(d) P(X + Y = 4). A coin is flipped until 3 heads in succession occur. List only those elements of the sample space that require 6 or less tosses. Is this a discrete sample space? Explain.The waiting time, in hours, between successive speeders spotted by a radar unit is a continuous random variable with cumulative distribution function Find the probability of waiting less than 12 minutes between successive speeders (a) using the cumulative distribution function of X; (b) using the probability density function of X. Determine the value c so that each of the following functions can serve as a probability distribution of the discrete random variable X: (a) f(x) = c(x2 + 4), for x = 0, 1, 2, 3; (b) f(x) = c() (->), for x = 0, 1, 2.Referring to Exercise 3.38, find (a) the marginal distribution of X; (b) the marginal distribution of Y. Reference: Exercise 3.38: If the joint probability distribution of X and Y is given by RX, y) = 30 Ity, for x = 0, 1, 2, 3; y = 0, 1, 2, find a) P(X $2, Y= 1); b) P(X >2, Y= 1); c) (c) P(X >Y):(d) P(X + Y = 4).\f