solve these

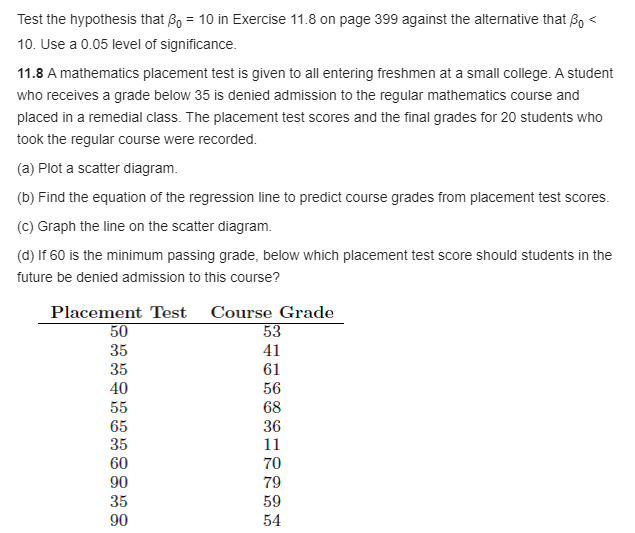
There are important applications in which, due to Known scientic constraints, the regression line must go through the origin he, the intercept must be zero}. In otherwords, the model should read Y :lfcaIea, i:l,2,...,n, and only a simple parameter requires estimation. The model is often called the regression through the origin model. {a} Show that the least squares estimator of the slope is in : imam i133 1121 11:1 2 2 2 {DjiShowthat 0'31 2 0' Z 1121; . 12:1 {c} show that 111 in part {a} is an unbiased estimator for 51. That is, show crap = m. Test the hypothesis that ,8\". = 15 in Exercise 11.3 on page 399 against the alternative that 5o s 15. Use a (105 level of signirmance. 11.3 A mathematics plaoement test is given to all entering freshmen at a small college. A student who receives a grade below 35 is denied admission to the regular mathematics course and placed in a remedial class. The placement test scores and the nal grades for 20 students who took the regular course were reoorded. {a} PM a scatter diagram. {on} Find the equation of the regression line to predict course grades from placement test scores. {c} Graph the line on the scalter diagram. {d} If ED is the minimum passing grade, below which placementtest score should students in the future DE UEHiEU admission 10 this EDUFSE? Placement Test Course Grade 51] 53 35 41 35 51 41] 55 55 53 55 35 35 l 1 51] TD t] 73 35 59 9|] 54 \fUse the data from Exercise "LED on page 342. {a} Estimate 02 using the multiple regression of y on 1'1, 1'2, and x3. {o} Compute a 95% prediction intenral for the observed gain with the three regressers at 11 = 15o, x2 = ssoo, and x3 = so. \fConsider a 2nd-order response surface model that contains the linear, pure quadratic and crossproduct terms as follows: 2 y. = n + .31311- + .3232.- + .31111a + .52421'5. + 31:31:12..- + Ea. Fit the model above to the followi ng data, and suggest an}:r model editing that may he needed. 1'1 1': y 1 l 35.33 1 l] 33.42 1 l 42.15 I] l 35.52 I] E] 45.2? I] l 53.22 1 l 3?.13 1 l] 43.25 1 1 55.0? A new curing process developed for a certain type of cement results in a mean compressive strength of 5000 kilograms per square centimeter with a standand deviation of 12d kilograms. To test the hypothesis that pr = sooo against the altemaljve that pr a: 5, a random sample of 50 pieces of cement is tested. The critical region is dened to be it st: 4970. {a} Find the probability of committing a type I error 1llvhen Hi] is true. {h} Evaluate 18 for the altemaijves ,u = 49m and p = 495D