Solving a maze problem with python:

A brief description of the problem:

Here you will solve a maze problem. You have to find the shortest path in the maze from a start node to the end node.

The problems description

For this problem, there are four moves (left, right, up, and down) from a maze position provided a valid step is available. In red square positions, no movement is allowed (like in start position only down motion is available since up and left move are blocked by the wall while for the right is a red square position thus no movement allowed).

First, we will create a class for a node that will contain all the attributes associated with the node like the parent of the node, position of the node, and all three costs (g,h & f) for the node. We initialize the node and build a method for checking the equality of the node with another node.

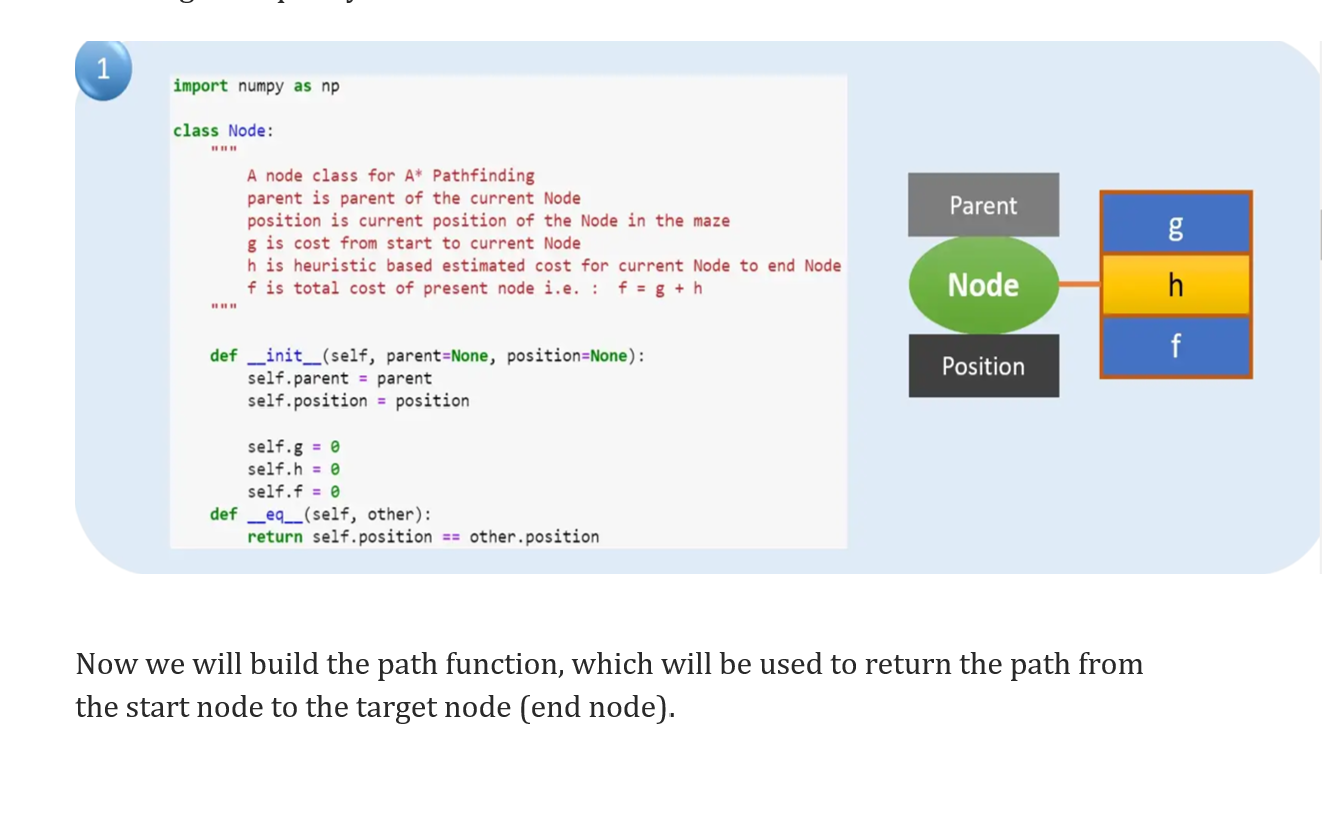
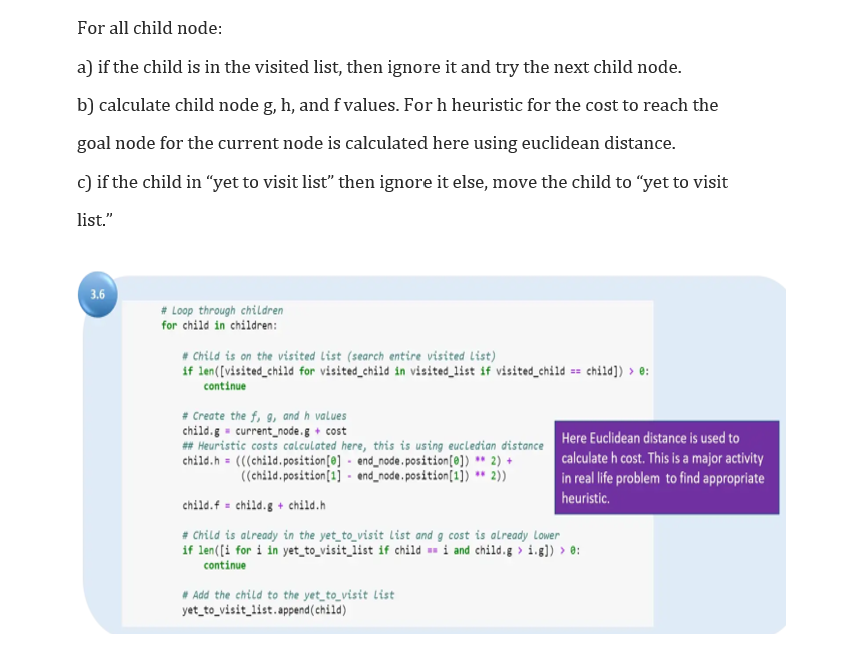
import numpy as np class Node: A node class for A Pathfinding parent is parent of the current Node position is current position of the Node in the maze g is cost from start to current Node h is heuristic based estimated cost for current Node to end Node f is total cost of present node i.e. : f=g+h def _init__lself, parent=None, position=None): self.parent = parent self.position = position self.g =0 self.h =0 self.f =0 def _eq_(self, other): return self.position == other.position Now we will build the path function, which will be used to return the path from the start node to the target node (end node). This function return the path of the search def return_path(current_node, maze): path = [] " here we create the initialized result maze with -1 in every position result = [[-1 for i in range(no_columns) ] for j in range(no_rows) ] while current is not None path. append(current. position) W. Return reversed path as we path = path [::-1] start_value we wate the for 1 in range(len(path)) result[path[i][e] return result Now we will define the search function, which has multiple steps. The first step will be to initialize nodes and lists that we will use in the function. Add the starting node to the "yet to visit list." Define a stop condition to avoid an infinite loop. Define movement in terms of relative position, which will be used to find the child node and other relative positions. \# Add the stort node yet_to_visit_list, append(start_node) - Adding a stop condition. This is to avoid any infinite loop and stop * execution after some reasonable number of steps outer_iterations = max_iterations = (len(maze) //2) * 10 - whot squares do we search, serarch movenent is left-right-top-bottom * (4 movements) from every positon nove=[[1,],#goup[,1],#g0left[1,0],#g0doin[0,1]]g0right Now we use the current node by comparing all f cost and selecting the lowest cost node for further expansion. We also check max iteration reached or not, Set a message and stop execution (avoid infinite loop) 3.3 "find maze has got how many rows and columns no_rows, no_columns = np. shape(maze) F Loop until you find the end while len(yet_to_visit_list) > : " Every time any node is referred from yet_to_visit list, counter of limit operation incremented outer_iterations +=1 \# Get the current node current_node = yet_to_visit_1ist[0] current_index = for index, item in enumerate(yet_to_visit_1ist): if item.f \& current_node.f: current_node =i ten current__index = index - if we hit this point return the path such as it may be no solution or - computation cost is too high If outer_iterations > max_iterations: print ("giving up on pathfinding too many iterations") return return_path(current_node, maze) Remove the selected node from "yet to visit list" and add this node to the visited list. Now we put a check if we found the target square. If we have located the target square, then call the path function and return. - Pop current node out off yet_to_visit list, odd to visited list yet_to_visit_1ist.pop(current_index) visited_1ist. append (current_node) Here we maintain which next node - test if goal is reached or not, if yes then return the path if current_node we end_node: return return_path(current_node, maze) For the selected node, find out all children (use the move to find children). Get the current position for the selected node (this becomes the parent node for the children) a) check if a valid location exists (boundary wall will make few nodes invalid) b) if any node position is invalid (red square) then ignore that c) add to valid children node list for the selected parent Here in the diagram, we show the black circle node is the current node, and green circle nodes are correct children node. 3.5 - Generate children from all adjacent squares children =[] for new_position in move: \# Get node position node_position = (current_node.position[e] + new_gosition[e], current_node.position[1] + now_gosition[1]) \# Make sure within range (check if within maze boundary) if (node_position[e] > (no_rows - 1) or node_position[e] or node_position [1] > (no_columns 1 ) or node_gosition [1] : continue " Create the f,g, and h values child.g = current_node.g + cost \#\# Heuristic costs calculated here, this is using eucledian distance Here Euclidean distance is used to ((child. position[1] - end_node.position[1]) * 2)) in real life problem to find appropriate child. f= child .8+ child.h heuristic. \# Child is already in the yet_to_visit list and g cost is already lower if len ([i for i in yet_to_visit_list if child =i and child,g >i,g])> : continue " Add the child to the yet_to_visit list yet_to_visit_list.append(child) Now finally, we will run the program from the main with the maze and obtain the path. Refer to the path also shown using the arrow. 4 if \( -^{\text {name_ }}={ }^{2} \) '_main_': Assessment: 1-You are required to implement this lab and submit your work showing the code and results. 2- You may try to use a different distance measure as (Manhattan distance )