
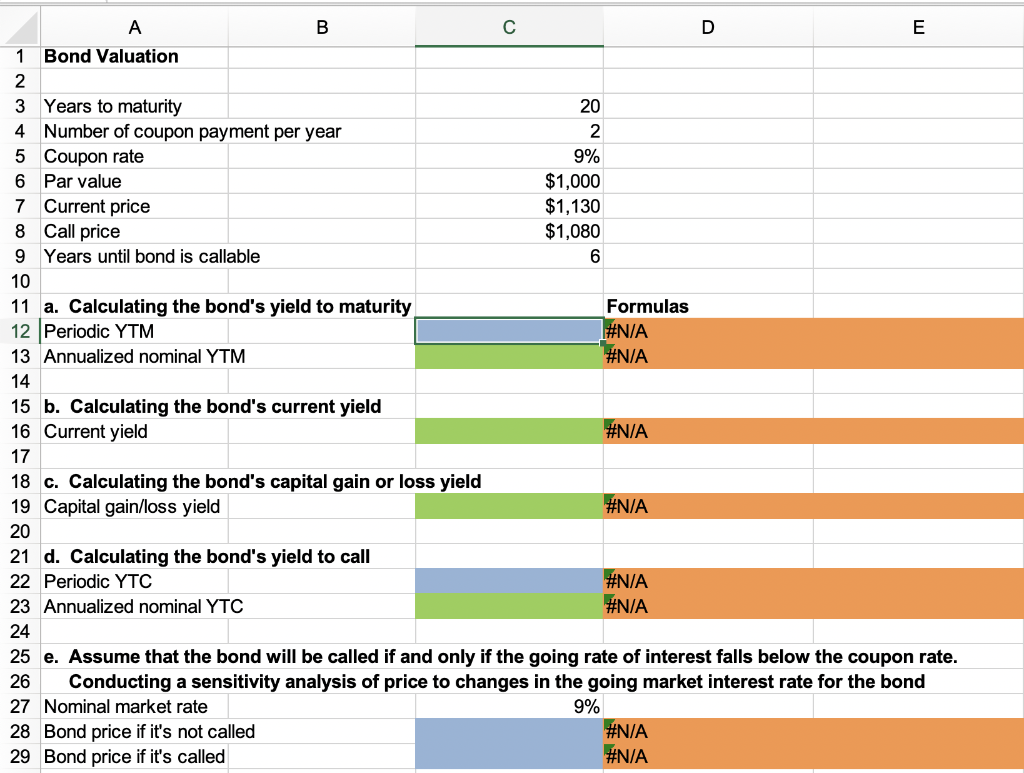
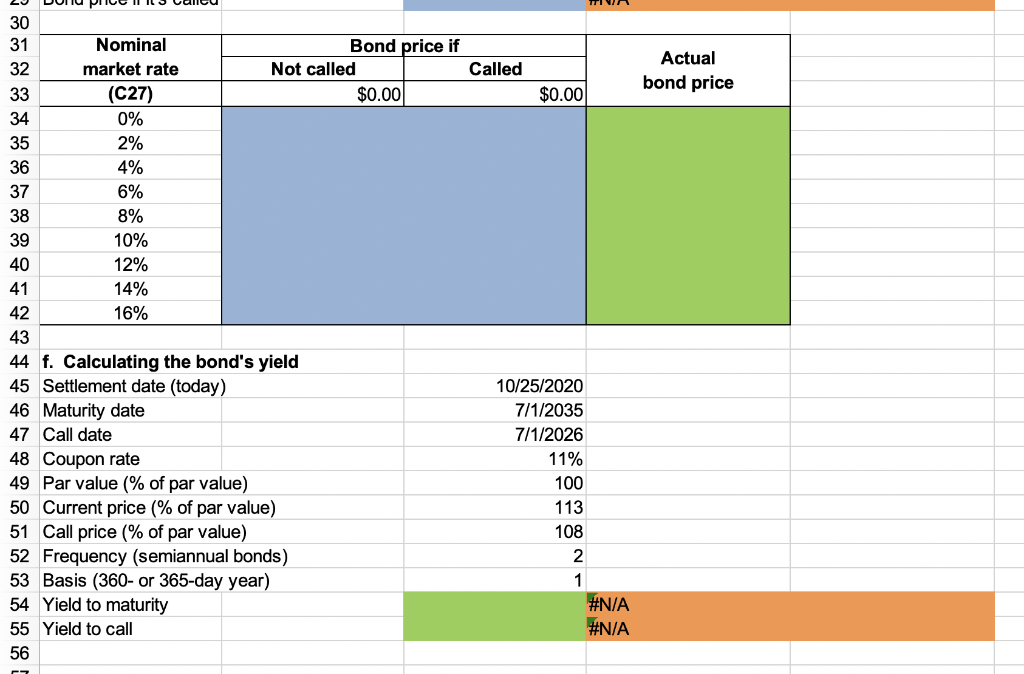
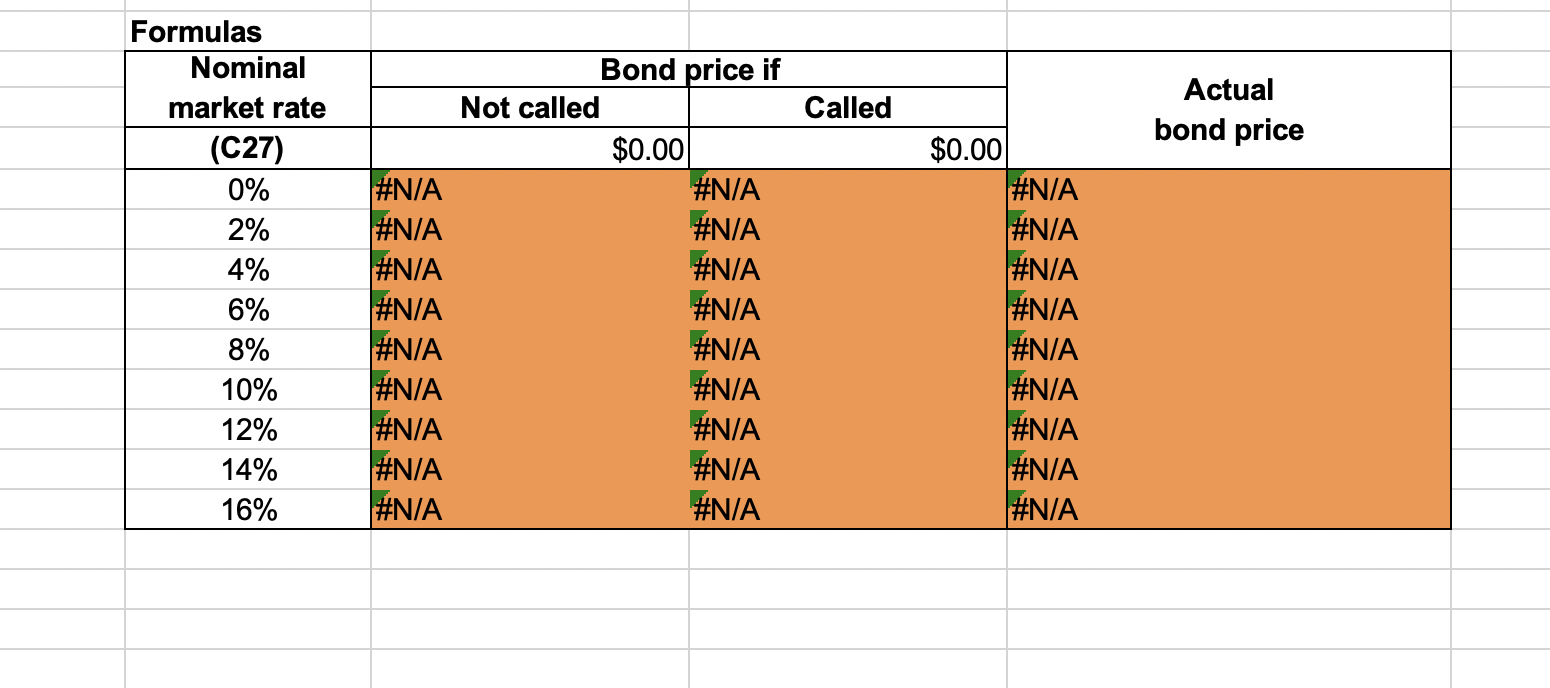



Start with the partial model in the file Ch04 P24 Build a Model.xlsx . A 20-year, 9% semiannual coupon bond with a par value of $1,000 may be called in 6 years at a call price of $1,080. The bond sells for $1,130. (Assume that the bond has just been issued.) The data has been collected in the Microsoft Excel file below. Download the spreadsheet and perform the required analysis to answer the questions below. Do not round intermediate calculations. Download spreadsheet Ch04 P24 Build a Model-ace579.xlsx A B D E 1 Bond Valuation WN 3 Years to maturity 20 4 Number of coupon payment per year 2 5 Coupon rate 9% 6 Par value $1,000 7 Current price $1,130 8 Call price $1,080 9 Years until bond is callable 6 10 11 a. Calculating the bond's yield to maturity Formulas 12 Periodic YTM #N/A 13 Annualized nominal YTM #N/A 14 15 b. Calculating the bond's current yield 16 Current yield #N/A 17 18 c. Calculating the bond's capital gain or loss yield 19 Capital gain/loss yield #N/A 20 21 d. Calculating the bond's yield to call 22 Periodic YTC #N/A 23 Annualized nominal YTC #N/A 24 25 e. Assume that the bond will be called if and only if the going rate of interest falls below the coupon rate. 26 Conducting a sensitivity analysis of price to changes in the going market interest rate for the bond 27 Nominal market rate 9% 28 Bond price if it's not called #N/A 29 Bond price if it's called #N/A Actual bond price 30 31 Nominal Bond price if 32 market rate Not called Called 33 (C27) $0.00 $0.00 34 0% 35 2% 36 4% 37 6% 38 8% 39 10% 40 12% 41 14% 42 16% 43 44 f. Calculating the bond's yield 45 Settlement date (today) 10/25/2020 46 Maturity date 7/1/2035 47 Call date 7/1/2026 48 Coupon rate 11% 49 Par value (% of par value) 100 50 Current price (% of par value) 113 51 Call price (% of par value) 108 52 Frequency (semiannual bonds) 2 53 Basis (360- or 365-day year) 1 54 Yield to maturity #N/A 55 Yield to call #N/A 56 Called Actual bond price Formulas Nominal market rate (C27) 0% 2% 4% 6% 8% 10% 12% 14% 16% Bond price if Not called $0.00 #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A $0.00 #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A a. What is the bond's yield to maturity? Round your answer to two decimal places. % b. What is the bond's current yield? Round your answer to two decimal places. % c. What is the bond's capital gain or loss yield? Round your answer to two decimal places. Use a minus sign to enter a negative value, if any. % d. What is the bond's yield to call? Round your answer to two decimal places. % e. How would the price of the bond be affected by a change in the going market interest rate? (Hint: Conduct a sensitivity analysis of price to changes in the going market interest rate for the bond. Assume that the bond will be called if and only if the going rate of interest falls below the coupon rate. This is an oversimplification, but assume it for purposes of this problem.) Round your answers to the nearest cent. Nominal market rate Actual bond price 0% $ 2% $ 4% $ 6% $ 8% $ 10% $ 12% $ 14% $ 16% $ f. Now assume the date is October 25, 2020. Assume further that an 11%, 15-year bond was issued on July 1, 2020, pays interest semiannually (on January 1 and July 1), and sells for $1,130. Again, it may be called in 6 years from the date of issue at a call price of $1,080. Use your spreadsheet to find the bond's yield. Round your answers to two decimal places. Yield to maturity: % Yield to call: %













