Question
Stationarity is established by running the Augmented Dickey-Fuller Test on the returns time series. The null hypothesis of the Augmented Dickey-Fuller is that the time
Stationarity is established by running the Augmented Dickey-Fuller Test on the returns time series.
The null hypothesis of the Augmented Dickey-Fuller is that the time series is non-stationary or the presence of unit-root in the time series. Since the p-value from the test is less than 0.05 the null hypothesis can be rejected, establishing that the time series is stationary. Stationary time series indicated that the different properties like mean, variance, and covariance do not depend on the time of observation.
Interpret the ACF and PACF plots from the following figures 
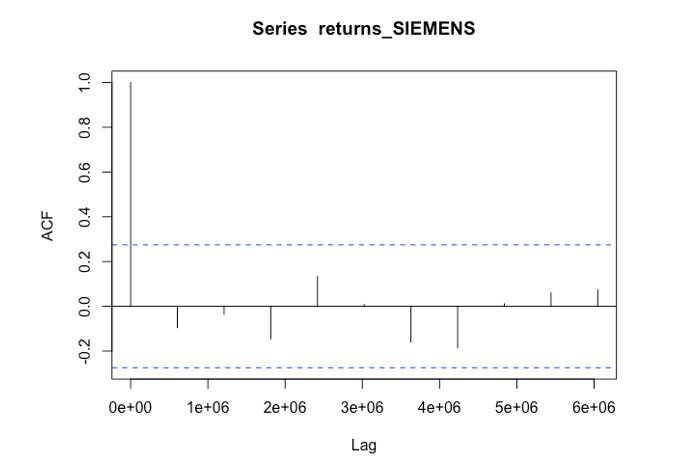
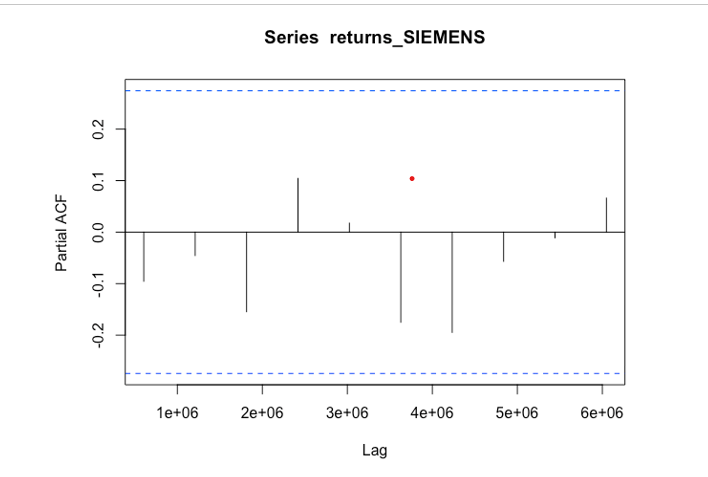
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


