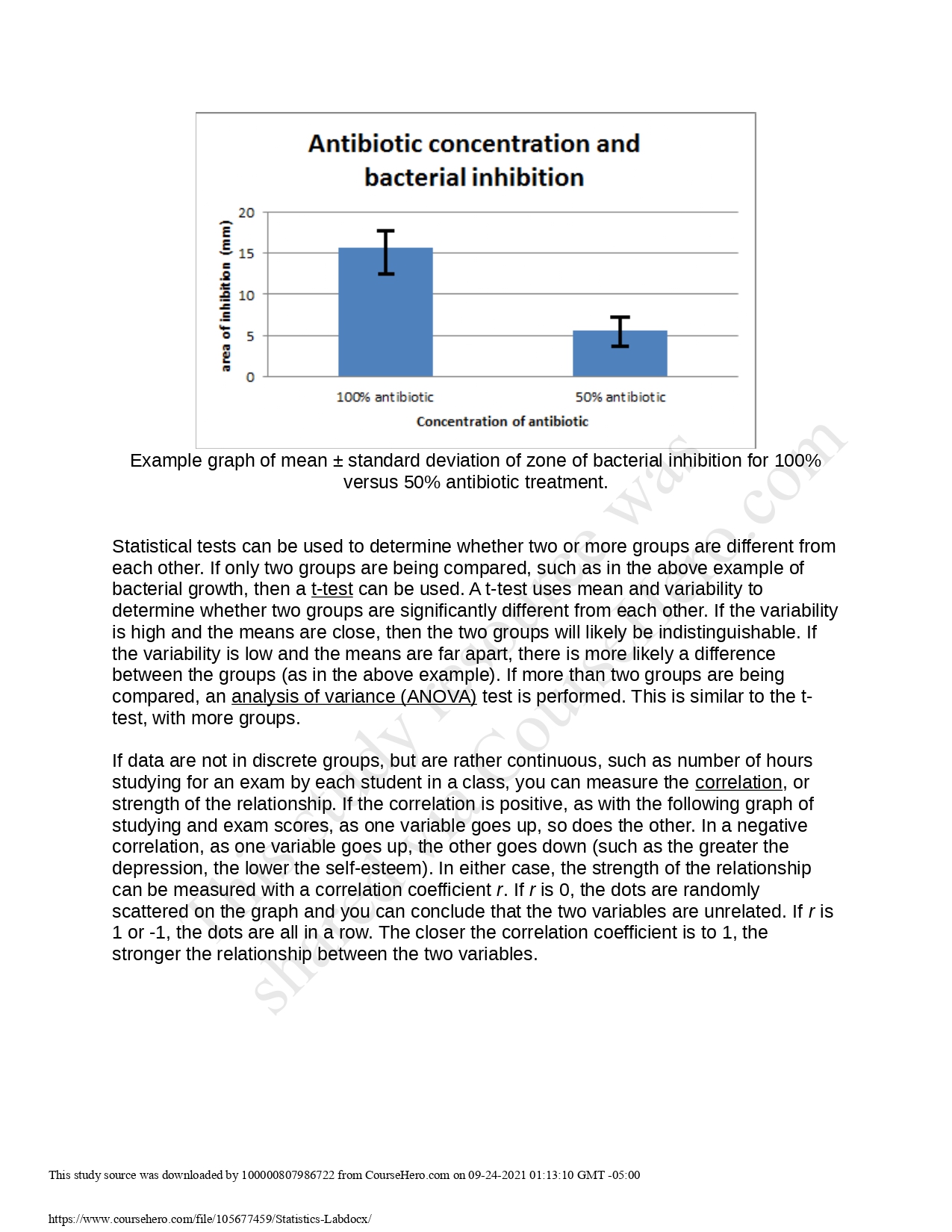
Statistical Literacy To learn basic statistics required for interpreting physiology studies Background: The majority of scientific studies contain a significant statistical component. We will be analyzing scientific studies in future labs, so a basic understanding of statistics is important. General Instructions: Read \"Basic Statistics" on the following pages before coming to class. We will discuss this in class. You will then work with your assigned lab group to answer questions. Full sentences for questions are not required unless you are asked to explain something to a patient. Submit one document per group on canvas. Lab Activity: Basic Statistics Statistics serves a number of purposes. First, it condenses large amounts of raw data into one or a few meaningful figures. Second, it facilitates the comparison between different sets of observations. It allows scientists to test hypotheses and predict future trends. As statistics are heavily used in scientific studies, and since these studies are used to make health care decisions, it is imperative that all students entering the health care field understand statistics. The mean, is the numerical center of the data, or the average. The standard deviation (SD) is the variation around the mean. If data are highly variable, the standard deviation will be large as well. Roughly 68% of the data fall within 1 standard deviation of the mean, and 95% of the data fall within 2 standard deviations of the mean. Outliers are values that fall several standard deviations above or below the mean. For example, the mean for an exam is 75 points. If the standard deviation is 2, that would mean that almost everyone got a C on that exam. If the standard deviation is 12, that would mean that some people got very low scores and others very high. The mean and standard deviation are often depicted in a bar graph as the bar height (mean) and error bars above and below the mean. In the example below of the effect of antibiotic concentration on bacterial inhibition, the bars represent the mean area of inhibition, and error bars show the size of one standard deviation, above and below the mean. If the error bars do not overlap significantiy, then the two groups are likely different from each other. In this context, it would mean that a 100% concentration of the antibiotic inhibited more bacteria than a 50% concentration. This study source was downloaded by 10000080798672 'om CourseHeropom on 09242021 01: 13: 10 GMT 05:00 httszr'wwwpourseherooom'lef 10567745 QIStattshcsLabdocxf Antibiotic concentration and bacterial inhibition an: oflnhiblinl (mm) 1M6 antibiotic 50% antibiotic Concentration of antibiotic Example graph of mean 1r standard deviation of zone of bacterial inhibition for 100% versus 50% antibiotic treatment. Statistical tests can be used to determine whether two or more groups are different from each other. If only two groups are being compared, such as in the above example of bacterial growth, then a M can be used. At-test uses mean and variability to determine whether two groups are significantly different from each other. If the variability is high and the means are close, then the two groups will likely be indistinguishable. If the variability is low and the means are far apart, there is more likely a difference between the groups (as in the above example). If more than two groups are being compared, an analysis of variance (ANOVA) test is performed. This is similar to the t- test, with more groups. If data are not in discrete groups, but are rather continuous, such as number of hours studying for an exam by each student in a class, you can measure the correlation, or strength of the relationship. If the correlation is positive, as with the following graph of studying and exam scores, as one variable goes up, so does the other. In a negative correlation, as one variable goes up, the other goes down (such as the greater the depression, the lower the self-esteem). In either case, the strength of the relationship can be measured with a correlation coefficient r. If r is 0, the dots are randomly scattered on the graph and you can conclude that the two variables are unrelated. If r is 1 or -1, the dots are all in a row. The closer the correlation coefficient is to 1, the stronger the relationship between the two variables. This study source was downloaded by 10000080798672 'om CourseHerocom on 09242021 01:13:10 GMT 05:00 https: waw. ooursehero .oorxlt'lefJ 10 567745 9fStattsl1csLabdocxf Effect of numbers of hours studying on exam grade 100 Q 30 . o E 60 E 40 7 .5 2D 0 0 5 10 15 20 25 30 Numberof hours studied Example graph of numbers of hours studied and exam grade. Many studies want to consider the effect of more than one variable on their parameter of interest. For example, if you are curious about the factors affecting exam scores, you are interested in number of hours studied, but also number of hours of sleep, number of hours of work, and number of hours of partying. These can all be factored in with an analysis called a regression. A regression analysis will tell you which of the factors actually best predict the exam score. Remember, however, that correlation is not causation! The graph above might mean that increasing the number of hours a particular student studies will increase her exam grades, but it might not. It is also possible that the type of people who study for many hours are the type of people who score well on exams, even though the extra study hours themselves are making no difference. The actual cause of the higher exam grades could be something else that people who tend to study more have in common, like a high degree of interest in the material, good writing skills, or paying attention in class. These other variables are called confounders, because they can confound, or confuse the findings. Another test commonly performed in medicine is the chi-square test. This test is used to determine whether there is a significant difference between the expected data and the observed data, so that you can test whether your data t your hypothesis. Hazard ratios are often used in medical research when there is a risk of a negative outcome. The hazard ratio is set to 1 for no increased risk. If the hazard ratio of a certain outcome (for example, cancer) is greater than 1, it means that there is an increased risk of that outcome. It the hazard ratio for a certain outcome (for example, osteoporosis) is less than 1, there is a decreased risk of that outcome. Statistical tests are used to determine the percent chance that there is no effect of your treatment. They do not give you a definitive answer. Look at the first graph comparing antibiotic treatments. Does it definitively prove that the concentration of antibiotic This study source was downloaded by 10000080798672 'om CourseHerdoom on 09242021 01: 13: 10 GMT 05:00 https: fr'www. ooursehero .oomflef 10 567745 QIStattstlcsLabdocxf makes a difference? The answer is no. There is always the possibility that what looks like a difference is actually random luck. Statistics can be used to measure the percent chance that that the groups you are testing are NOT actually different and that the difference is a result of chance. This percent chance is called the pvalue. Scientists have arbitrarily set the acceptable p-value for calling a result \"statistically significant" at 0.05 (or 5%). This means that if the p-value is above 0.05 (say 0.1, a 10% chance that the groups are not different), we are not confident enough to say that the groups are indeed different. However, if the p-value is below 0.05 (say 0.01, or a 1% chance of no difference), then we ARE confident enough to call the result statistically significant. Significant p-values are often marked with asterisks above the bars. If multiple groups or factors are all being tested at the same time, we must be more conservative with the p-value to decrease the number of incorrect conclusions. This is when corrections are made to the p-value for multiple comparisons. These corrections are referred to by names such as Tukey, Schefie, and Bonferroni. You have now learned about p-value, which is statistical significance. However, it is important to keep in mind that a statistically significant (i.e., non-random) effect can also be extremely small, or even irrelevant. Thus, it is at least equally important to consider biological significance. This refers to whether the nding is important, and includes factors to consider such as the magnitude and relevance of the effect, as well as how the effect was achieved (how much of what kind of treatment), and any negative side effects. For example, a study might find that eating five pounds of carrots a day causes statistically significant weight loss. Is it time for the carrot diet? What if the average weight loss after eight weeks was .02 pounds, the incidence of diarrhea was 75%, and the incidence of carotenemia (yellow skin pigmentation) was 69%? In addition to biological significance, you should also consider the scope of inference, which is the population to which the study pertains. If the study was done on lab rats, is it necessarily applicable to humans? If the study was done on middle-aged Caucasian women, is it necessarily applicable to men? Young women? People of Asian descent? Last, consider any study biases. There are two main forms of error in a scientific study. Random error occurs when the groups do not consist of clones, as is most often the case. You are studying the effect of vitamin D on development of cancer, and there are people in each group that are closet smokers, or that eat a heavier meat diet than others. Studies should attempt to minimize this form of error by screening because it increases variability and makes it harder to get a significant p-value. However, this form of error is normal and not lethal to a study. In fact, with a large sample size, the effect of this error decreases. The other form of error, systematic error, is lethal to a study because it introduces bias. This occurs when the group compositions are different in a way that was not intended. For example, when studying the effect of vitamin D on cancer, if you place all of the vegetarians in the vitamin D group and all of the meat eaters in the placebo group, you will no longer be able to determine whether any difference between the groups is due to \ tamin D, or to their diet. In sum, systematic error leads to bias, making it impossible to draw conclusions about the experiment. This study source was downloaded by 10000050793672 from Comalierooom on 09242021 01: 13: 10 GMT 705:00 hltpsjr'www.oomsehero_oomfle-'10567745 9r"Statiir.t:Lcs7LalxiooipIr Questions: 1-5. Consider the following data graph: Zinc and duration of cold symptoms Duration of cold symptoms, days OHNW with zinc without zinc Figure 1: Mean + SD duration of cold symptoms in days with zinc or with placebo. Asterisks denote statistically significant differences at p