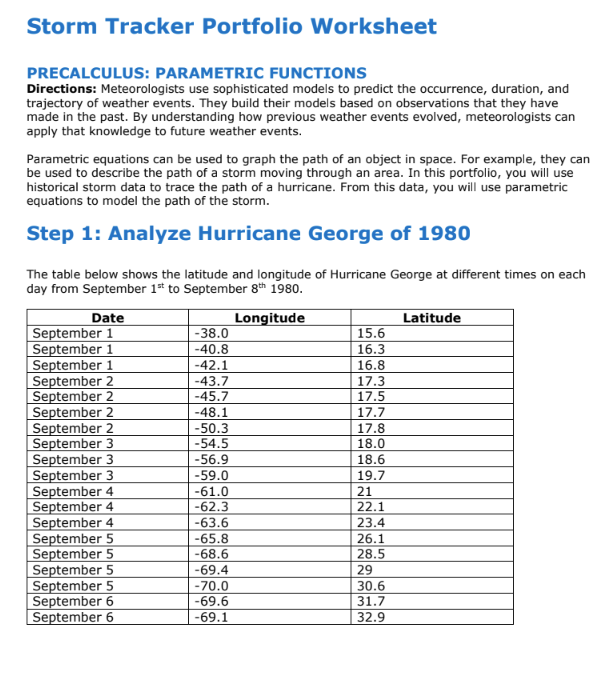
Storm Tracker Portfolio Worksheet PRECALCULUS: PARAMETRIC FUNCTIONS Directions: Meteorologists use sophisticated models to predict the occurrence, duration, and trajectory of weather events. They build their models based on observations that they have made in the past. By understanding how previous weather events evolved, meteorologists can apply that knowledge to future weather events. Parametric equations can be used to graph the path of an object in space. For example, they can be used to describe the path of a storm moving through an area. In this portfolio, you will use historical storm data to trace the path of a hurricane. From this data, you will use parametric equations to model the path of the storm. Step 1: Analyze Hurricane George of 1980 The table below shows the latitude and longitude of Hurricane George at different times on each day from September 1" to September 8th 1980. Date Longitude Latitude September 1 -38.0 15.6 September 1 -40.8 16.3 September 1 -42.1 16.8 September 2 -43.7 17.3 September 2 -45.7 17.5 September 2 -48.1 17.7 September 2 -50.3 17.8 September 3 -54.5 18.0 September 3 -56.9 18.6 September 3 -59.0 19.7 September 4 -61.0 21 September 4 -62.3 22.1 September 4 -63.6 23.4 September 5 -65.8 26.1 September 5 -68.6 28.5 September 5 -69.4 29 September 5 - 70.0 30.6 September 6 -69.6 31.7 | September 6 -69.1 32.9 Step 2: Plot the Hurricane Path Use the data from step 1 to make a table of the storm's horizontal and vertical movement with respect to time. Start with a data point provided in the table in step 1 from September 1 and make this date t = 0. Note the position's longitude and latitude and record them in Table 1. Since latitude measures north/south and longitude measures east/west, the latitude coordinate will be y and the longitude coordinate will be x. Now progress through the days along the path. Choose and record one point from each day of the storm. Mark each point t = 1, t = 2, etc. Track the storm for a total of 6 days so that you have 6 points in the table, one from each day of the storm. For example: Pick one of the data points for September 1 This point is t = 0 Record the x (longitude) and y (latitude) coordinates in Table 1 Pick one of the data points for September 2. This point is t=1 Record the x (longitude) and y (latitude) coordinates in Table 1 Repeat for September 3rd, 4th, 5th and 6th which will be t=2, 3, 4, 5 Table 1 Actual data collected x and y Date t x (longitude) y (latitude) (East/West) (North/South) 0 1 2 3 4 5 Step 3: Create a Mathematical Model Work through the following steps to create two parametric equations where x is a function of t and y is a function of t. Remember t is just a parametric variable. You are creating two functions x(t) and y(t) ***If you use a linear regression for this portfolio the highest grade you are able to earn is a 70*** a. Plot x (longitude is the vertical axis) versus t (horizontal axis) (1 point) b. Ploty (latitude is the vertical axis) versus t horizontal axis. These should be two separate graphs. Make sure to submit the 2 graphs for your instructor to view. Label your axes and chose appropriate scales and ranges for your axis. (1 point) c. What type of function or regression model do you think would best fit the data based on your graphs? (1 points) What type of function will you be using for x (longitude versus t). What type of function will you be using for y (latitude versus t) Use your calculator to create a formula for the model you have chosen. Enter the ordered pairs into lists and have the calculator create the best fit function for your model. For example, if your path appears to be exponential, you will have a model of the form y=ab using the ExpReg feature on the calculator. If you think the function is quadratic your model will have the form y = at? + bt + c using the QuadReg feature on the calculator. You will then do the same for x. You do not have to use the same model type for both x and y. Pick the model that fits each one best! Remember do not use a linear function! Directions to create this model on the T184Plus Calculator at end of portfolio. d. Write your final equations: (2 points) X(t) = . y(t) = Step 4: Use your Parametric Model to find the predicted x and y at each time point. Using your equations you found in step 3 to find the predicted x and y coordinates. Plug in the values t = 0, 1, 2, 3, and 4 into your parametric equations and enter your values for x and y in the table below. Table 2 Predicted x & y from your model's equation (2 points) t x (longitude) predicted from model y (latitude) predicted from model 0 1 2 3 4 5 a. Plot your predicted x (table 2) and your actual x (table 1) versus time on one graph. The vertical axis is the longitude, and the horizontal axis is t. (1 pt) b. Plot predicted y (table 2) and your actual y (table 1) versus time on one graph. The vertical axis is latitude and the horizontal axis is t. (1 pt). Make sure to submit the 2 graphs and label your axes and chose appropriate scales and ranges. Have a key indicating which data are predicted and which are actual. For example use one color for predicted and one color for actual. C. Visually compare the actual and predicted data on the plots? Do they seem to be similar? If not consider using a different model and repeating part 3d and Step 4. Step 5: Check your Parametric Model Now graph the actual x- and y-coordinates from Table 1 using one color and graph the predicted or modeled x- and y-coordinates from Table 2 onto the same graph using a different color. Your x coordinates are the horizontal axis and your y coordinates are the vertical axis. Be sure to label which color is which dataset. You may either copy and paste your graph here or upload it along with this worksheet. 1. How does your model compare to the actual path? Be specific and write at least 2 sentences supporting your conclusion (1 pt) 2. Why did you choose the graph family that you did? Did you choose well? Why or why not? (1 pt) 3. Is it possible to write this in rectangular form, eliminating the parameter t. In other words express y in terms of x (eliminate the parameter t and have one function, y =f(x)) Why or why not? (1 pt)