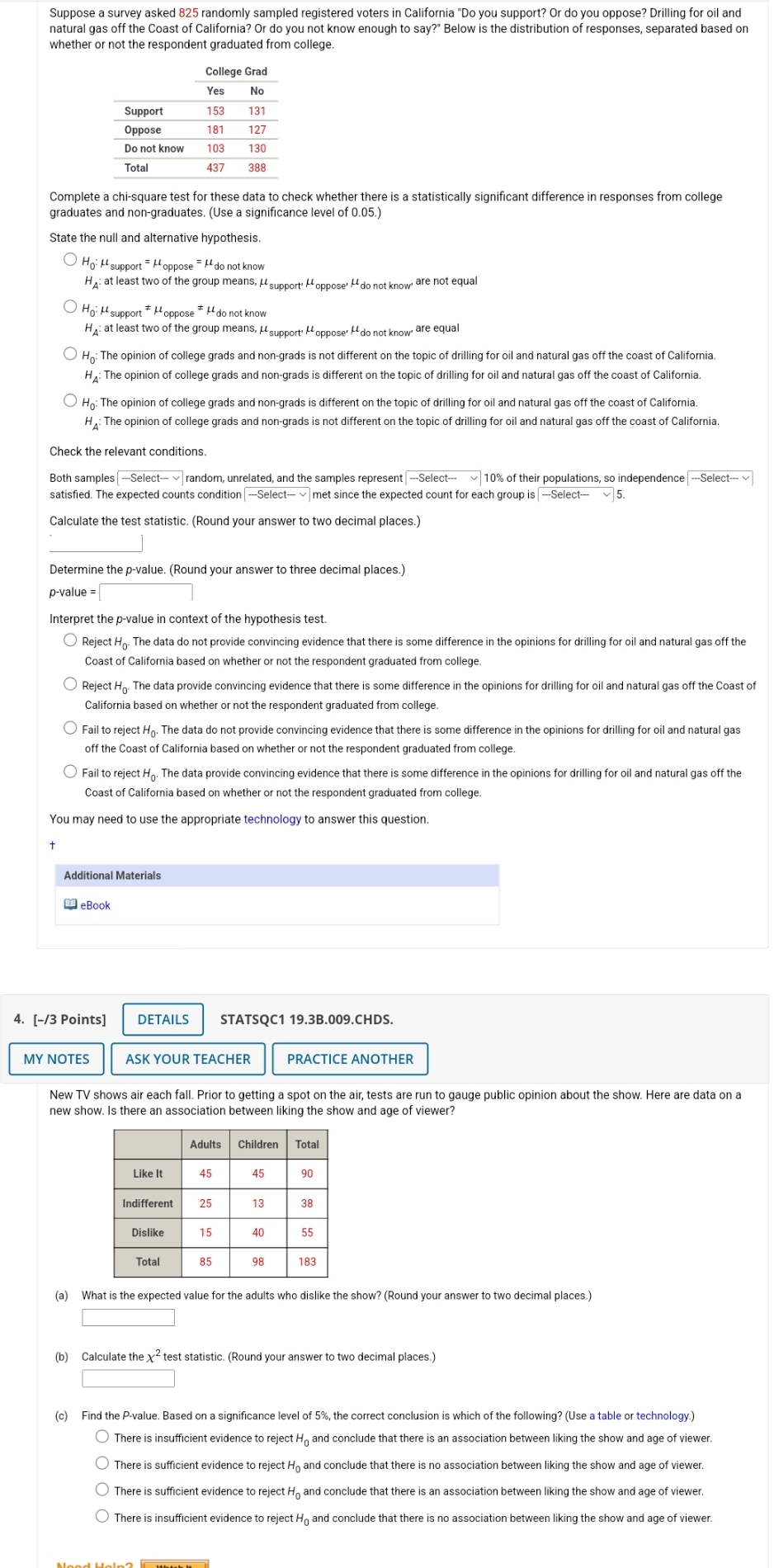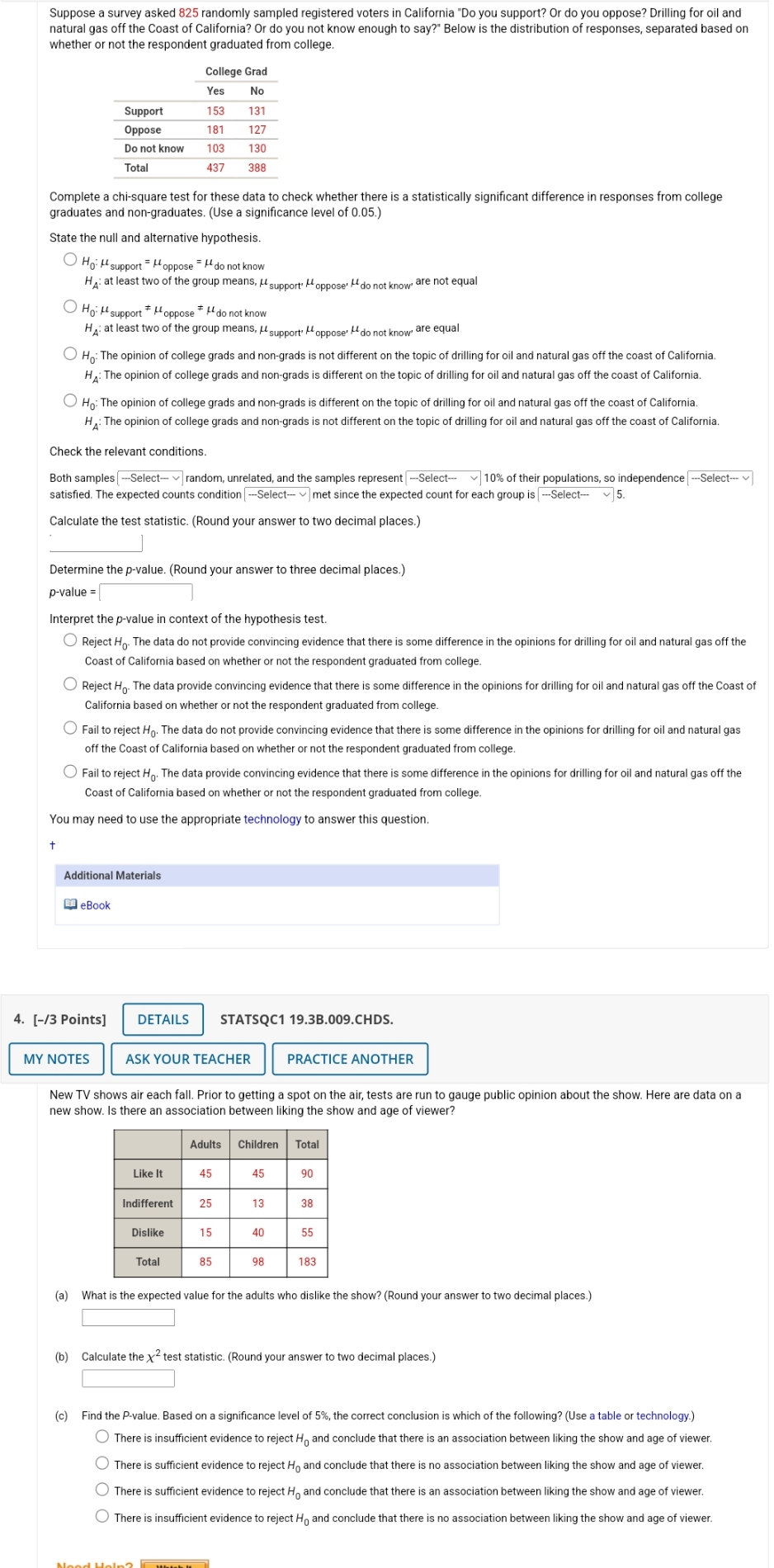
Suppose a survey asked 825 randomly sampled registered voters in California "Do you support? Or do you oppose? Drilling for oil and natural gas off the Coast of California? Or do you not know enough to say?" Below is the distribution of responses, separated based on whether or not the respondent graduated from college. College Grad Yes No Support 153 131 Oppose 181 127 Do not know 103 130 Total 437 388 Complete a chi-square test for these data to check whether there is a statistically significant difference in responses from college graduates and non-graduates. (Use a significance level of 0.05.) State the null and alternative hypothesis. O Ho: H support = H oppose = I do not know H: at least two of the group means, I support' oppose' I do not know are not equal O Ho: H support * H oppose * I do not know H,: at least two of the group means, I support' oppose' At do not know are equal O Ho: The opinion of college grads and non-grads is not different on the topic of drilling for oil and natural gas off the coast of California. HA: The opinion of college grads and non-grads is different on the topic of drilling for oil and natural gas off the coast of California. O Ho: The opinion of college grads and non-grads is different on the topic of drilling for oil and natural gas off the coast of California. HA: The opinion of college grads and non-grads is not different on the topic of drilling for oil and natural gas off the coast of California. Check the relevant conditions. Both samples |-Select- | random, unrelated, and the samples represent | -Select-- |10% of their populations, so independence --Select-- satisfied. The expected counts condition | --Select- | met since the expected count for each group is | --Select- ~]5. Calculate the test statistic. (Round your answer to two decimal places.) Determine the p-value. (Round your answer to three decimal places.) p-value = Interpret the p-value in context of the hypothesis test. Reject Ho. The data do not provide convincing evidence that there is some difference in the opinions for drilling for oil and natural gas off the Coast of California based on whether or not the respondent graduated from college. Reject Ho. The data provide convincing evidence that there is some difference in the opinions for drilling for oil and natural gas off the Coast of California based on whether or not the respondent graduated from college. Fail to reject Ho. The data do not provide convincing evidence that there is some difference in the opinions for drilling for oil and natural gas off the Coast of California based on whether or not the respondent graduated from college. Fail to reject Ho. The data provide convincing evidence that there is some difference in the opinions for drilling for oil and natural gas off the Coast of California based on whether or not the respondent graduated from college. You may need to use the appropriate technology to answer this question. Additional Materials eBook 4. [-/3 Points] DETAILS STATSQC1 19.3B.009.CHDS. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER New TV shows air each fall. Prior to getting a spot on the air, tests are run to gauge public opinion about the show. Here are data on a new show. Is there an association between liking the show and age of viewer? Adults Children Total Like It 45 45 90 Indifferent 25 13 38 Dislike 15 55 Total 183 (a) What is the expected value for the adults who dislike the show? (Round your answer to two decimal places.) (b) Calculate the x2 test statistic. (Round your answer to two decimal places.) (c) Find the P-value. Based on a significance level of 5%, the correct conclusion is which of the following? (Use a table or technology.) There is insufficient evidence to reject Ho and conclude that there is an association between liking the show and age of viewer. There is sufficient evidence to reject Ho and conclude that there is no association between liking the show and age of viewer. There is sufficient evidence to reject Ho and conclude that there is an association between liking the show and age of viewer. There is insufficient evidence to reject Ho and conclude that there is no association between liking the show and age of viewer