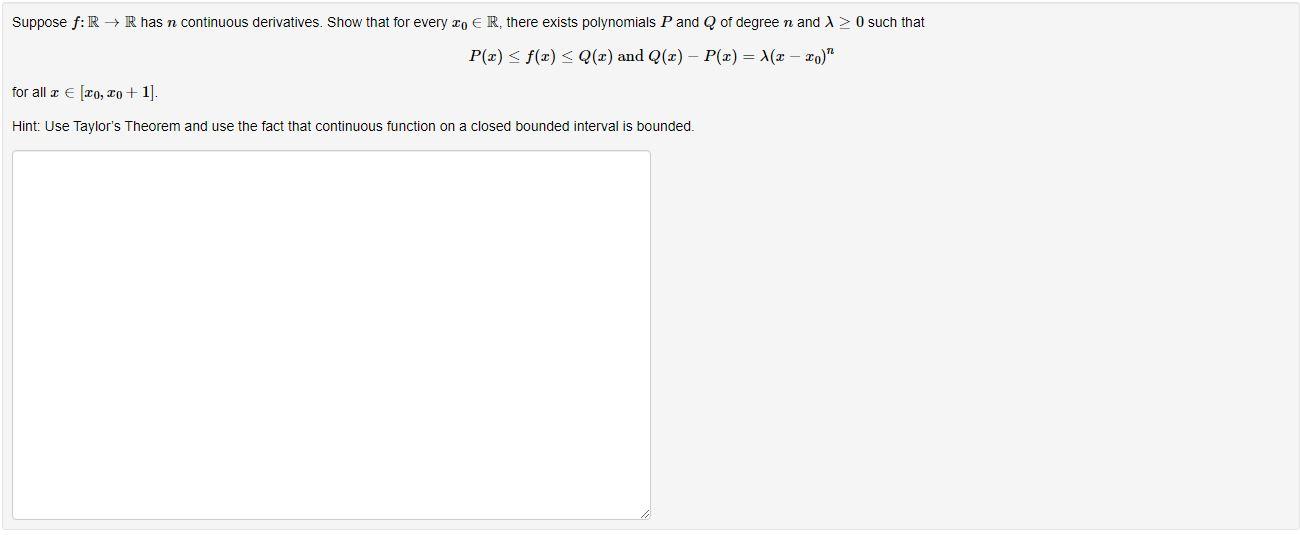
Suppose f: R R has n continuous derivatives. Show that for every To ER, there exists polynomials P and Q of degree n and > 0 such that P(x) f(x) Q(x) and Q(x) - P(x) = x(x xo)" for all x [2o, co + 1]. Hint: Use Taylor's Theorem and use the fact that continuous function on a closed bounded interval is bounded.