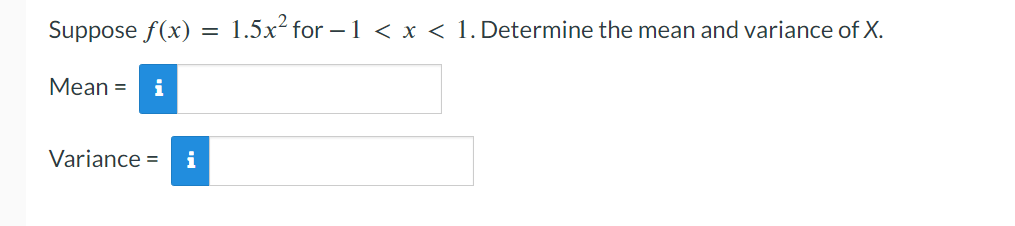
Question: Suppose f(x) = 1.5x for 1 < x < 1. Determine the mean and variance of X. Mean = i Variance = i The


Suppose f(x) = 1.5x for 1 < x < 1. Determine themean and variance of X. Mean = i Variance = i Thetime to failure (in hours) for a laser in a cytometry machineis modeled by an exponential distribution with = 0.00004. Round the answers

Suppose f(x) = 1.5x for 1 < x < 1. Determine the mean and variance of X. Mean = i Variance = i The time to failure (in hours) for a laser in a cytometry machine is modeled by an exponential distribution with = 0.00004. Round the answers to 3 decimal places. (a) What is the probability that the laser will last at least 20457 hours? i (b) What is the probability that the laser will last at most 30608 hours? i (c) What is the probability that the laser will last between 20457 and 30608 hours? i Suppose the counts recorded by a Geiger counter follow a Poisson process with an average of two counts per minute. Round the answers to 3 decimal places. (a) What is the probability that there are no counts in a 30-second interval? i (b) What is the probability that the first count occurs in less than 9 seconds? i (c) What is the probability that the first count occurs between 1 and 2 minutes after start-up? i Assume the flaws along a magnetic tape follow a Poisson distribution with a mean of 0.5 flaw per meter. Let X denote the distance between two successive flaws. (Round your answer to 4 decimal places.) (a) What is the mean of X? (b) What is the probability that there no flaws in 10 consecutive meters of tape? (a) i (b) i

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Mechanical Engineering Questions!

Q:

Add or subtract as indicated. 1 x - 1 x 1 I

Q:

MUST BE CORRECT ANSWERS A small software company has the following simplified cashflow, funded by shareholders' equity of 20,000 and a bank overdraft of 5000: Invoiced money received 2 months after...

Q:

can someone solve this Modern workstations typically have memory systems that incorporate two or three levels of caching. Explain why they are designed like this. [4 marks] In order to investigate...

Q:

Use f= 0.5 Please please clear and correct 100% answer And all details and show when you solve the numbers using if. And with clear hand writing. Please Q4 Three electron emitters produce electron...

Q:

Math 181 Exam I (Summer 2015/2016) Name: Exam Coverage: Midterm Exam 1 covers material from Units 1-3. Specifically, you should be familiar with topics from chapters 1.1, 1.2, 10.1, 10.2, and 10.3....

Q:

Calculus Writing Assignment: Fundamental Theorem of Calculus, Part 2 Each portion of a problem is worth 5 points. Total Points: 50 Answer each of the problems. Make sure to show all your work. x...

Q:

4. (30 points) Let us hypothetically assume that the weekly demand of water at a market, D, follows a uniform distribution, U (20000, 40000). (Let the unit of D be gallons.) We know that the mean of...

Q:

Basic Calculus, Derivative Rules MULTIPLE CHOICE: Write the capital letter of the best answer in the space provided before the number. 1. Suppose f (x) = x2 (x2 + 1), determine f'(2) ? A. 48 B. 36 C....

Q:

can you please help me with these practice questions. 1. Suppose approximately 59% of all students study after midnight. For random sample ofn=3students, letXbe the number of students that study...

Q:

Suppose f (x) = x 3 + 2x 2 x + 6. From calculus, the Mean Value Theorem guarantees that there is at least one number in the open interval ( 1, 2) at which the value of the derivative of f, given by...

Q:

5. Athens Development Corporation is considering a new product that will be sensitive to both economic conditions and competitor response. The product manager has decided to focus on three economic...

Q:

For each of the transactions in E1-34B, tell whether the transaction was an operating, investing, or financing activity. In E1-34B, 1. Izzy started the business by contributing $5,500 in exchange for...

Q:

Let s make some decisions based on a brief financial statement & ratio analysis. Using the information provided for ABC Company below, and considering the lecture material from Week 6 , along with...

Q:

Prospect Realty Co. pays weekly salaries of $27,600 on Monday for a six-day workweek ending the preceding Saturday. Journalize the necessary adjusting entry at the end of the accounting period,...

Q:

Refer to Problem 27. The default multiplicative decomposition in Minitab assumes a linear trend. Fit and plot a linear trend line to the Wal-Mart sales. Is a linear trend appropriate for these data?...

Q:

Table P-27 gives quarterly sales (in millions of dollars) for Wal-Mart Stores from 1990-2004. Use Minitab to do a multiplicative decomposition of the Wal-Mart sales time series for the years...

Q:

Indicate with a Yes or No whether or not each of the following accounts normally requires an adjusting entry: a. Building b. Cash c. Interest Expense d. Miscellaneous Expense e. Nancy Palmer, Capital...

Q:

The quarterly sales levels (measured in millions of dollars) for Goodyear Tire are shown in Table P-13. Does there appear to be a significant seasonal effect in these sales levels? Analyze this time...

Q:

2 . 2 ) Find the equation for the set of all points equidistant from the planes y = 2 and y = - 4 . The equation for the set of all points equidistant from the planes is ( Type an equation. )

Q:

All cable television companies carry at least one home-shopping channel. Who uses these home-shopping services? Are the shoppers primarily men or women? Suppose you want to estimate the difference in...

Q:

In Teaching of Psychology (Aug. 1998), a study investigated whether final exam performance is affected by whether or not students take a practice test. Students in an introductory psychology class at...

Q:

A version of the dice game "craps" is played in the following manner. A player starts by rolling two balanced dice. If the roll (the sum of the two numbers showing on the dice) results in a 7 or 11,...

Q:

=+1. General-purpose resistors are color-coded with a sequence of four rings that identify the nominal value of the resistance (in ohms) and the plus and minus tolerance (expressed as a percentage of...

Q:

39. Consider a bookbag filled with 100 poker chips. You know that either 70 of the chips are red and the remainder blue, or that 70 are blue and the remainder red. You must guess whether the bookbag...

Q:

42. Suppose that the payoff functions of two actions are P (oi, y) = 50 + .5y and P(a2, y) = 70 .5/x, where y is the mean of a normal process with variance 1200. (a) Find the breakeven value, /i&....