Suppose that a firm has N large rolls of paper, each W inches wide. It is necessary to cut Ni rolls of width Wi from these rolls of paper. We can formulate this problem by defining variables

 xij = Number of smaller rolls of width Wi cut from large roll j.

We assume there are m different widths Wi . In order to cut all the required rolls of width Wi , we need constraints of the form:

Further, the number of smaller rolls cut from a large roll is limited by the width W of the large roll. Assuming no loss due to cutting, we have constraints of the form:

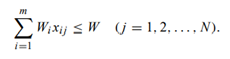
a) Formulate an objective function to minimize the number of large rolls of width W used to produce the smaller rolls.

 b) Reformulate the model to minimize the total trim loss resulting from cutting. Trim loss is defined to be that part of a large roll that is unusable due to being smaller than any size needed.

 c) Comment on the difficulty of solving each formulation by a branch-and-bound method.

 d) Reformulate the problem in terms of the collection of possible patterns that can be cut from a given large roll. (Hint. See Exercise 25 in Chapter 1.)

e) Comment on the difficulty of solving the formulation in (d), as opposed to the formulations in (a) or (b), by a branch-and-bound method.

N * = N (i =1,2,...,m).