


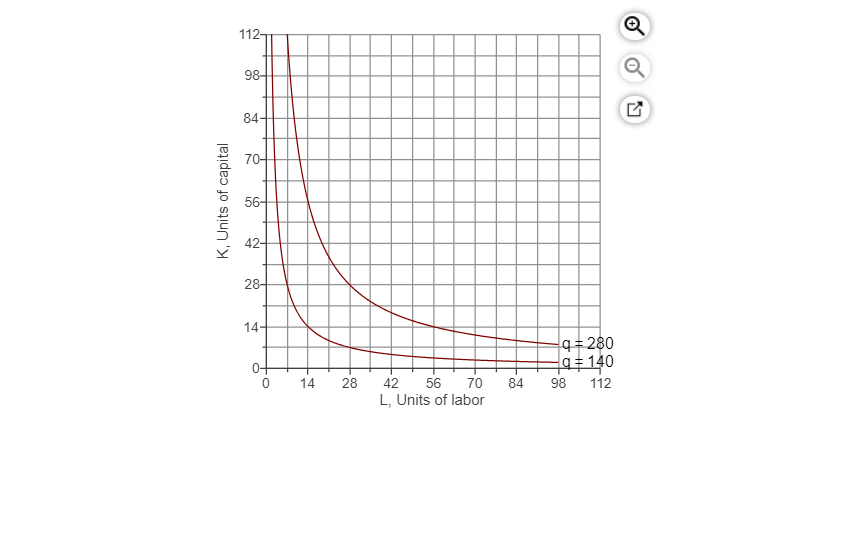
Suppose that a firm's production function is: q= 10L0.560.5 Using calulus we know that its marginal product functions are: .5, 0.5 5K0.5L MP = = 0.5g/L and MPK = 5L 0.5/K0.5 = 0.5g/K. The cost of a unit of labor, w, is $50 and the cost of a unit of capital, r, is $50. The isoquants for output of 140 and 280 are illustrated in the figure to the right 1. Initially, the firm is producing 140 units of output and has determined that the cost-minimizing quantities of labor and capital are 14 and 14, respectively. Suppose now that the firm wants to increase output to 280 units. If capital is fixed in the short run, how much labor will the firm require? The firm will now require units of labor. (Enter your response rounded to two decimal places.) 2. The firm's marginal rate of technical substitution is MRTS = (Enter your response as a function of K and L.) Hence, the tangency condition is (Enter your response as an equation in terms of K and L.) In addition, to be able to produce 280 units of output, K and L must also satisfy (Enter your response as an equation in terms of K and L.) Solving the two equations above gives that the optimal combination of capital and labor required to produce the 280 units of output is units of capital and units of labor. (Enter your responses as integers.) Does the short-cut for Cobb-Douglas function to slove for optimal bundle applies here? (Hint: check if the ratio of labor cost to capital cost is the same as the ratio of the two power coefficients in the prodution function.) Yes No 3. Plot the cost-minimizing levels of capital and labor along with the isocost lines corresponding to outputs of 140 and 280 units 1.) Using the point drawing tool, plot the cost-minimizing quantities of labor and capital at 14 and 14 (Suppose that the firm is producing 140 units of output.) Label this point E1 2.) Using the line-drawing tool, draw the corresponding isocost line. Label this line 1 3.) Using the point-drawing tool, plot the cost-minimizing quantities of labor and capital that you found earlier in the problem. (Suppose the firm increases output to 280 units.) Label this point E2 4.) Using the line-drawing tool, draw the corresponding isocost line. Label this line C2- Carefully follow the instructions above, and only draw the required objects. 112 Q 98- 84 70- K Units of capital 56 42 28+ 14- o+ 4+280 9140 98 112 14 28 42 56 70 L, Units of labor 84 Suppose that a firm's production function is: q= 10L0.560.5 Using calulus we know that its marginal product functions are: .5, 0.5 5K0.5L MP = = 0.5g/L and MPK = 5L 0.5/K0.5 = 0.5g/K. The cost of a unit of labor, w, is $50 and the cost of a unit of capital, r, is $50. The isoquants for output of 140 and 280 are illustrated in the figure to the right 1. Initially, the firm is producing 140 units of output and has determined that the cost-minimizing quantities of labor and capital are 14 and 14, respectively. Suppose now that the firm wants to increase output to 280 units. If capital is fixed in the short run, how much labor will the firm require? The firm will now require units of labor. (Enter your response rounded to two decimal places.) 2. The firm's marginal rate of technical substitution is MRTS = (Enter your response as a function of K and L.) Hence, the tangency condition is (Enter your response as an equation in terms of K and L.) In addition, to be able to produce 280 units of output, K and L must also satisfy (Enter your response as an equation in terms of K and L.) Solving the two equations above gives that the optimal combination of capital and labor required to produce the 280 units of output is units of capital and units of labor. (Enter your responses as integers.) Does the short-cut for Cobb-Douglas function to slove for optimal bundle applies here? (Hint: check if the ratio of labor cost to capital cost is the same as the ratio of the two power coefficients in the prodution function.) Yes No 3. Plot the cost-minimizing levels of capital and labor along with the isocost lines corresponding to outputs of 140 and 280 units 1.) Using the point drawing tool, plot the cost-minimizing quantities of labor and capital at 14 and 14 (Suppose that the firm is producing 140 units of output.) Label this point E1 2.) Using the line-drawing tool, draw the corresponding isocost line. Label this line 1 3.) Using the point-drawing tool, plot the cost-minimizing quantities of labor and capital that you found earlier in the problem. (Suppose the firm increases output to 280 units.) Label this point E2 4.) Using the line-drawing tool, draw the corresponding isocost line. Label this line C2- Carefully follow the instructions above, and only draw the required objects. 112 Q 98- 84 70- K Units of capital 56 42 28+ 14- o+ 4+280 9140 98 112 14 28 42 56 70 L, Units of labor 84










