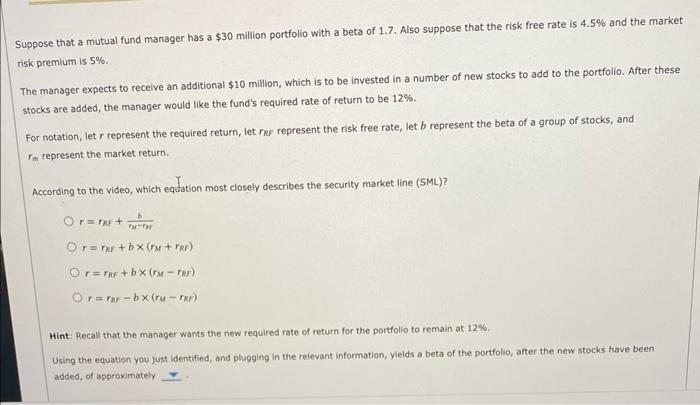
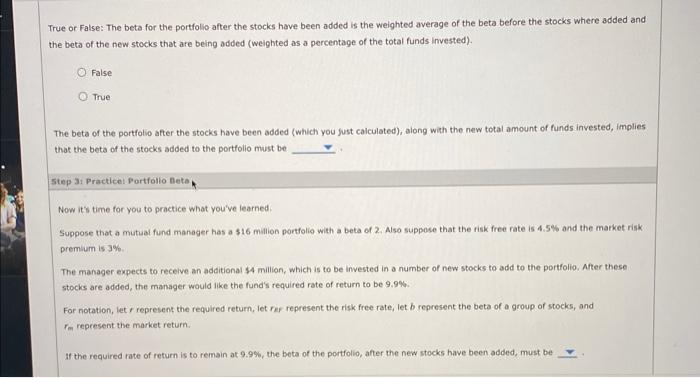
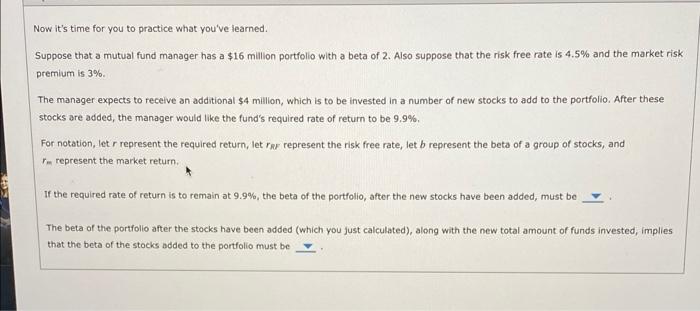
Suppose that a mutual fund manager has a $30 million portfolio with a beta of 1.7. Also suppose that the risk free rate is 4.5% and the market risk premium is 5%. The manager expects to receive an additional $10 million, which is to be invested in a number of new stocks to add to the portfolio. After these stocks are added, the manager would like the fund's required rate of return to be 12%. For notation, let r represent the required return, let rRF represent the risk free rate, let b represent the beta of a group of stocks, and rm represent the market return. According to the video, which equation most closely describes the security market line (SML)? r=rRF+MMrEbr=rRF+b(rM+rRP)r=rBF+b(rMrRF)r=rMFb(rMrRR) Hint: Recall that the manager wants the new required rate of return for the portfolio to remain at 12%. Using the equation you just identified, and plugging in the relevant information, yields a beta of the portfolio, after the new stocks have been added, of approximately True or False: The beta for the portfolio-after the stocks have been added is the weighted average of the beta before the stocks where added and the beta of the new stocks that are being added (weighted as a percentage of the total funds invested). False True The beta of the portfolio after the stocks have been added (which you fust calculated), along with the new total amount of funds invested, implies thot the beta of the stocks added to the portfolio must be Step It Practicel fortfollo Beta Now it's time for you to practice what you've learned. Suppose that a mutual fund manager has a $16 million portfolia with a beta of 2. Also suppose that the risk free rate is 4.5% and the market risk premium is 3%. The manager expects to receive an additional \$4 miliion, which is to be invested in a number of new stocks to add to the portfolio, After these stocks are added, the manager would like the fund's required rate of return to be 9.9%. For notation, let r represent the required return, let res represent the risk free rate, let b represent the beta of a group of stocks, and rm represent the market return. If the required rate of return is to remain at 9.9%, the beta of the portfolio, after the new stocks have been added, must be Now it's time for you to practice what you've learned. Suppose that a mutual fund manager has a $16 million portfolio with a beta of 2 . Also suppose that the risk free rate is 4.5% and the market risk premium is 3%. The manager expects to receive an additional \$4 million, which is to be invested in a number of new stocks to add to the portfolio. After these stocks are added, the manager would like the fund's required rate of return to be 9.9%. For notation, let r represent the required return, let rRF represent the risk free rate, let b represent the beta of a group of stocks, and rmrrepresentthemarketreturn. If the required rate of return is to remain at 9.9%, the beta of the portfolio, after the new stocks have been added, must be The beta of the portfolio after the stocks have been added (which you just calculated), along with the new total amount of funds invested, implies that the beta of the stocks added to the portfolio must be