Question
Suppose that an Australian Company AA wants to build a supermarket in the United Kingdom and a British Company BB wants to do the same
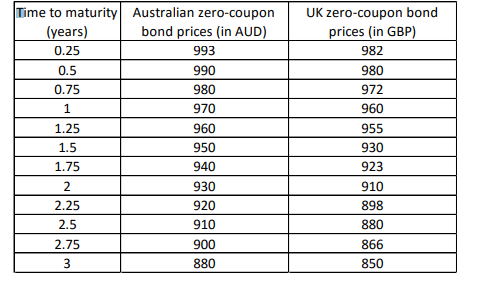
Suppose that an Australian Company AA wants to build a supermarket in the United Kingdom and a British Company BB wants to do the same in Australia. They both need local currency to pay for the investment. The two companies decide to take the loan in their own country in their own currency with a size equivalent to 200 million AUD and enter into a swap with a three-year term on a principal that equals to the size of their loan amount. The spot exchange rate is currently quoted at $2 per each pound. AA pays BB 4 percent per annum and BB pays AA 6 percent per annum. The swap payments occur semi-annually at the end of each half year. The zero-coupon bond prices of zero-coupon bonds in Australia and the United Kingdom with a face value of 1000 in its local currency at maturity are given below:
a) How is a currency swap different from a plain vanilla interest rate swap? (3 marks)
b) What is the principal for this currency swap? What are the principal-related cash flows in this swap contract between AA and BB? (3 marks)
c) Calculate the gross payments involved in this swap contract per period and indicate who pays what in this swap deal? (4 marks)
d) Would AA and BB agree to enter into this swap contract with the gross payments stated above? If not, what else is required to make them to be happy to enter into this swap contract? (6 marks)
e) Assume that the currency swap is fairly priced, in which situation AA would be more likely to be interested in raising funds for investment this way (i.e. take the loan in AUD then enter into a swap). (2 marks)
f) Using the information provided to calculate the forward exchange rate between AUD and GBP quoted in AUD-GBP for exchange 2 years from now? (2 marks)
UK zero-coupon bond prices (in GBP) 982 980 Time to maturity Australian zero-coupon (years) bond prices (in AUD) 0.25 993 0.5 990 0.75 980 1 970 1.25 960 1.5 950 1.75 940 2 930 2.25 920 2.5 910 2.75 900 3 880 972 960 955 930 923 910 898 880 866 850 UK zero-coupon bond prices (in GBP) 982 980 Time to maturity Australian zero-coupon (years) bond prices (in AUD) 0.25 993 0.5 990 0.75 980 1 970 1.25 960 1.5 950 1.75 940 2 930 2.25 920 2.5 910 2.75 900 3 880 972 960 955 930 923 910 898 880 866 850Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


