Suppose that (inverse)demand for Fortnite v-bucks is given by P(Q) = 20 - 1.35Q

BEFORE Epic's split with Apple: We know Apple charges a fee of 30% of Epic's revenue. Epic's revenue is (1 - 30%) x P(Q) x Q = 70% x (20 - 1.35Q) x Q. Epic's marginal cost is zero. Assume that Epic chooses its price like a monopolist (in this case, a monopolist facing a 'tax' by apple.) Assume that Apple faces no costs whatsoever, and this 'tax' it charges Epic is essentially free money for Apple.

AFTER Epic's split with Apple: Epic no longer has to pay Apple's 'tax'. Epic's revenue is P(Q) x Q= (100 - Q) x Q. Assume that Epic sets a price equal to 80% of the price it set before the split with Apple. This is the price that Epic has announced to the world. However, in our simple model, it is impossible for this to be a profit-maximizing price for Epic, as long as Epic's marginal costs are zero.

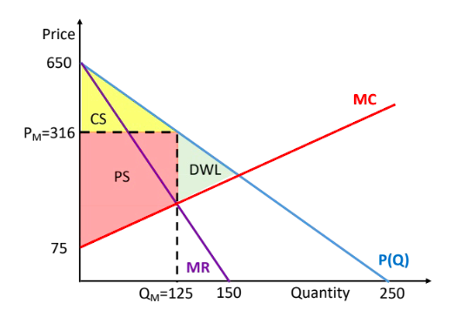
Draw a diagram for both situations: BEFORE the split with Apple, and AFTER the split with Apple. The diagrams should be similar to the example below