Question
Suppose that s is an irrational number and the sequence (r(n)) of rational numbers converges to s: r(n) = a(n) / b(n), where a(n) and
Suppose that s is an irrational number and the sequence (r(n)) of rational numbers converges
to s: r(n) = a(n) / b(n), where a(n) and b(n) are integers, b(n)>0. Show that b(n)??. In other words, the
only way to get a very good approximation to an irrational number by a rational number is to have a
large denominator..
ii. Show that there is a constant C such that if m and n are positive integers then |m - 2 |> C
n^2. (Hint: Consider the product (m - 2 )(m + 2 ). This cannot be 0. )
iii. Show that the product (x-
( 2 + 3 ?? ? ?x - ? 2 - 3 ??(?x - ?- 2 + 3 ??(?x - ?- 2 - 3 ?? is a polynomial with integer
coefficients. In other words, when you multiply it out the coefficients turn out to be integers.

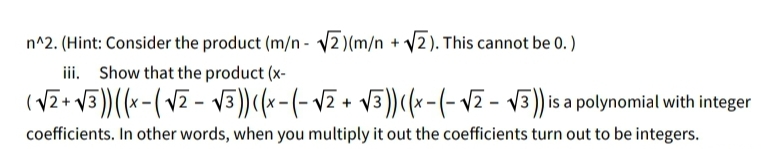
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


