
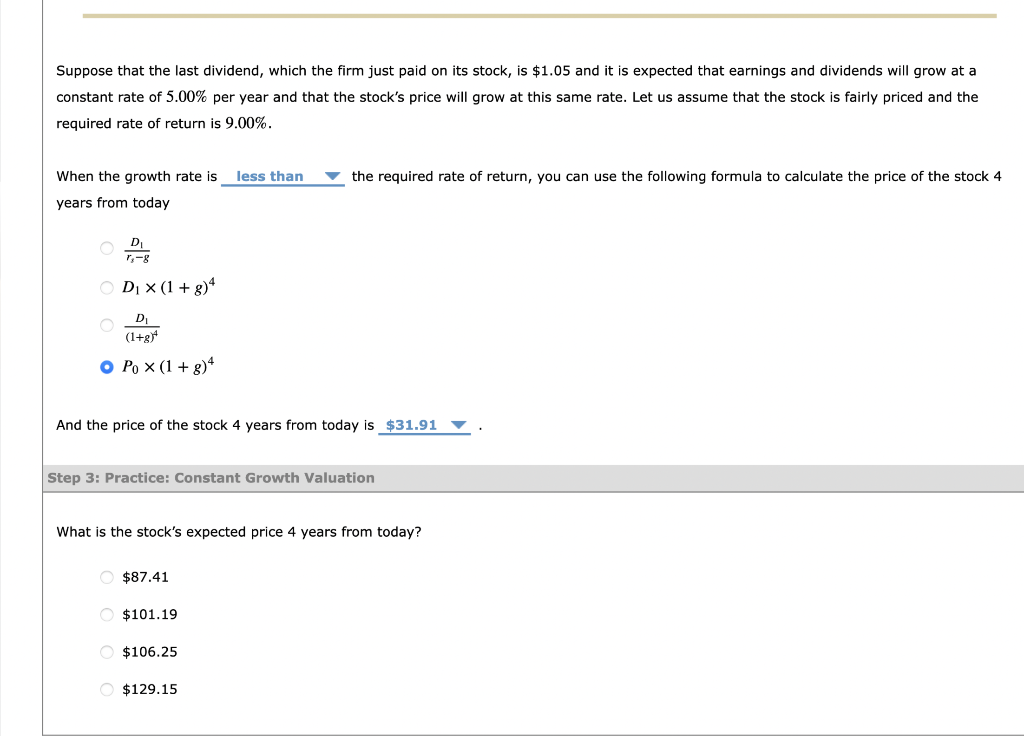
Suppose that the last dividend, which the firm just paid on its stock, is D0=$1.00 and the stock's last closing price is $26.25. It is expected that earnings and dividends will grow at a constant rate of g=5.00% per year and that the stock's price will grow at this same rate. that the stock is fairly priced, that is, it is in equilibrium, and the most appropriate required rate of return is rs=9.00%. The dividend received in period 1 is D1=$1.00(1+0.0500)=$1.05 and the estimated intrinsic value in the same period is based on the constant growth model: P1=rsgD2. Using the same logic, compute the dividends, prices, and the present value of each of the dividends at the end of The dividend yield for period 1 is and it will each period. The capital gain yield expected during period 1 is and it will each period. If it is forecasted that the total return equals 9.00% for the next 5 years, what is the forecasted total return out to infinity? 4.00% 5.00%9.00% 14.00% Note that this stock is called a "Hold" as its forecasted intrinsic value is equal to its current price P0=rsgD1=0.09000.0500$1.05=$26.25 and the expected total return is equal to the required rate of return rs. If the market was more optimistic and the growth rate would ber 6.00% rather than 5.00%, the stock's forecasted intrinsic value would be P0=0.09000.0600$1.05=$35.00, which is greater than $26.25. In this case, you would call the stock a "Buy". Suppose that the last dividend, which the firm just paid on its stock, is $1.05 and it is expected that earnings and dividends will grow at a constant rate of 5.00% per year and that the stock's price will grow at this same rate. Let us assume that the stock is fairly the required rate of return is 9.00%. When the growth rate is the required rate of return, you can use the following formula to calculate the price of the stock 4 years from today rsgD1D1(1+g)4(1+g)4D1P0(1+g)4 And the price of the stock 4 years from today is Step 3: Practice: Constant Growth Valuation What is the stock's expected price 4 years from today? $87.41 $101.19 $106.25 $129.15 Suppose that the last dividend, which the firm just paid on its stock, is D0=$1.00 and the stock's last closing price is $26.25. It is expected that earnings and dividends will grow at a constant rate of g=5.00% per year and that the stock's price will grow at this same rate. that the stock is fairly priced, that is, it is in equilibrium, and the most appropriate required rate of return is rs=9.00%. The dividend received in period 1 is D1=$1.00(1+0.0500)=$1.05 and the estimated intrinsic value in the same period is based on the constant growth model: P1=rsgD2. Using the same logic, compute the dividends, prices, and the present value of each of the dividends at the end of The dividend yield for period 1 is and it will each period. The capital gain yield expected during period 1 is and it will each period. If it is forecasted that the total return equals 9.00% for the next 5 years, what is the forecasted total return out to infinity? 4.00% 5.00%9.00% 14.00% Note that this stock is called a "Hold" as its forecasted intrinsic value is equal to its current price P0=rsgD1=0.09000.0500$1.05=$26.25 and the expected total return is equal to the required rate of return rs. If the market was more optimistic and the growth rate would ber 6.00% rather than 5.00%, the stock's forecasted intrinsic value would be P0=0.09000.0600$1.05=$35.00, which is greater than $26.25. In this case, you would call the stock a "Buy". Suppose that the last dividend, which the firm just paid on its stock, is $1.05 and it is expected that earnings and dividends will grow at a constant rate of 5.00% per year and that the stock's price will grow at this same rate. Let us assume that the stock is fairly the required rate of return is 9.00%. When the growth rate is the required rate of return, you can use the following formula to calculate the price of the stock 4 years from today rsgD1D1(1+g)4(1+g)4D1P0(1+g)4 And the price of the stock 4 years from today is Step 3: Practice: Constant Growth Valuation What is the stock's expected price 4 years from today? $87.41 $101.19 $106.25 $129.15








