Suppose that we want to estimate the effect of education on income using observational data. To do so, it is suggested to run a regression of the logarithm of income, 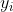, over schooling years, 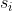, and another variable related with both education and income, say 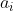, for "ability". Thus, the regression is:

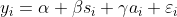
where 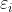is not correlated with 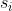or .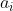

Consider the relationship of matching and regression with controls.

i) Suppose that there is only one covariate 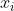and that it is binary. Additionally, asume the probability for an individual to receive the treatment is positive for both values of 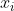. Derive the matching and regression coefficients.

ii) Prove that both matching and regression estimators are the same if the treatment is assigned randomly.

yi= a + Bsi+ya; + ; yi= a + Bsi+ya; +