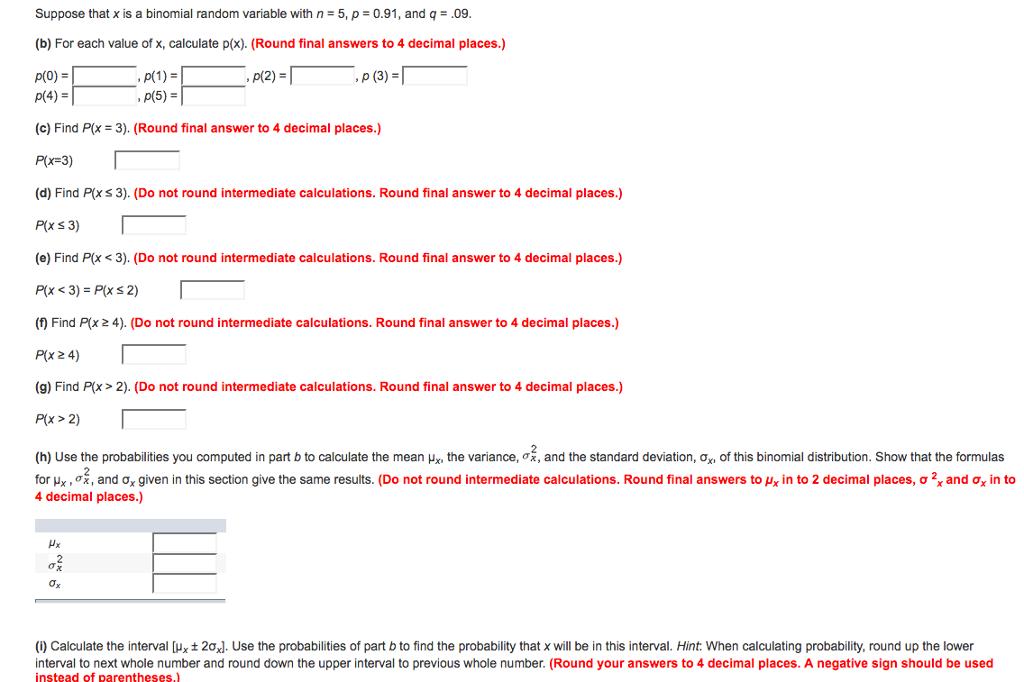
Suppose that x is a binomial random variable with n= 5, p = 0.91, and q = .09. (b) For each value of x, calculate p(x). (Round final answers to 4 decimal places.) p(0) = ,p(2) = ,p (3) = ,p(1) = p(5)= p(4)= (c) Find P(x = 3). (Round final answer to 4 decimal places.) P(x=3) (d) Find P(x 3). (Do not round intermediate calculations. Round final answer to 4 decimal places.) P(x 3) (e) Find P(x 2). (Do not round intermediate calculations. Round final answer to 4 decimal places.) P(x > 2) (h) Use the probabilities you computed in part b to calculate the mean ux. the variance, o, and the standard deviation, ox, of this binomial distribution. Show that the formulas for x, o, and ox given in this section give the same results. (Do not round intermediate calculations. Round final answers to u, in to 2 decimal places, o 2, and ox in to 4 decimal places.) Hx 0} Ox (i) Calculate the interval [ux 20%). Use the probabilities of part b to find the probability that x will be in this interval. Hint: When calculating probability, round up the lower interval to next whole number and round down the upper interval to previous whole number. (Round your answers to 4 decimal places. A negative sign should be used instead of parentheses.)